Question

如图，点M（，0）为Rt△OED斜边上的中点，O为坐标原点，∠ODE=90°，过D作AB⊥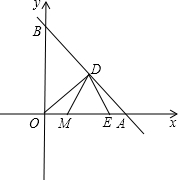DM交x轴的正半轴于A点，交y轴的正半轴于B点，且sin∠OAB=
（1）求：过E、D、O三点的二次函数解析式．
（2）问此抛物线顶点C是否在直线AB上，请予以证明；若顶点不在AB上，请说明理由．
（3）试在y轴上作出点P，使PC+PE为最小，并求出P点的坐标（不写作法和证明）

Answer 1

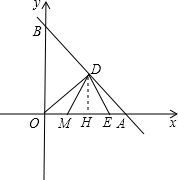解：作DH⊥x轴于H．
（1）∵点M（，0）为Rt△OED斜边上的中点，根据“直角三角形斜边上的中线等于斜边的一半”得OM=ME=DM=，
∴OE=×2=3，
得E（3，0）．
∵AB⊥DM，sin∠OAB=，
∴在Rt△ADM中，AM===．
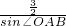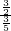根据勾股定理，AD=2，于是在Rt△DHA中，HD=2×sin∠OAB=2×=，
根据勾股定理，AH=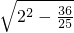=，OH=4-=．
于是D点坐标为（，）．
∵抛物线过E（3，0）、D（，）、O（0，0）三点，
∴设解析式为y=ax²+bx．
将各点代入解析式得：，
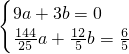解得a=-，b=，
解析式为y=-x²+x．

（2）∵DA=2，DM=，
∴根据勾股定理得，AM==，MO=，
∴AO=+==4，
∴得A（4，0）．因为直线过A（4，0）、D（，）两点，
设解析式为y=kx+b，
将A（4，0）、D（，）代入得，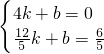
解得，
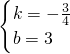直线解析式为y=-x+3．
由（1）知抛物线解析式为y=-x²+x，
顶点坐标为x=-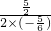=，y==，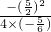
即C（，），
代入直线AB的解析式得，-×（）+3=，故顶点在AB上；

（3）作出E点关于y轴的对称点E′，
则E‘点坐标为（-3，0），直线CE′的解析式为y=kx+b，
将C（，）、E‘（-3，0）代入解析式
得，，
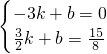解得，
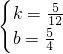解析式为y=x+，
当x=0时，y=，
即P点坐标为（0，）．
分析：（1）作DH⊥x轴于H，根据“直角三角形斜边上的中线等于斜边的一半”和sin∠OAB=，求出D点坐标和E点坐标，又知抛物线过点O，可设出二次函数一般式解答；
（2）求出抛物线顶点C的坐标和直线解析式，将顶点C代入直线解析式看是否成立；
（3）作出E点关于y轴的对称点E′，连接CE'与y轴交点即为点P，根据两点之间线段最短，存在点P使PC+PE’最小，根据轴对称的性质PC+PE最小．
点评：此题将直角三角形的性质和直线、抛物线相结合，巧妙利用了坐标和线段长度之间的关系，求出所需坐标，利用待定系数法求出函数解析式，利用解析式，其它问题便可迎刃而解．