题目内容
3.在一个不透明的盒子里,装有四个分别写有数字-2、-1、1、2的乒乓球(形状、大小一样),先从盒子里随机取出一个乒乓球,记下数字后放回盒子,然后搅匀,再从盒子里随机取出一个乒乓球,记下数字.(1)求一次取出乒乓球上的数字是负数的概率;
(2)求两次取出乒乓球上的数字之和等于0的概率.
(3)求两次取出乒乓球上的数字之积小于2的概率.
分析 (1)由在一个不透明的盒子里,装有四个分别写有数字-2、-1、1、2的乒乓球(形状、大小一样),直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次取出乒乓球上的数字之和等于0的情况,再利用概率公式即可求得答案;
(3)由(2)中的树状图可求得两次取出乒乓球上的数字之积小于2的情况,再利用概率公式即可求得答案.
解答 解:(1)∵在一个不透明的盒子里,装有四个分别写有数字-2、-1、1、2的乒乓球(形状、大小一样),
∴一次取出乒乓球上的数字是负数的概率为:$\frac{2}{4}$=$\frac{1}{2}$;
(2)画树状图得:
∵共有16种等可能的结果,两次取出乒乓球上的数字之和等于0的有4种情况,
∴两次取出乒乓球上的数字之和等于0的概率为:$\frac{4}{16}$=$\frac{1}{4}$;
(3)∵两次取出乒乓球上的数字之积小于2的有10种情况,
∴两次取出乒乓球上的数字之积小于2的概率为:$\frac{10}{16}$=$\frac{5}{8}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
15.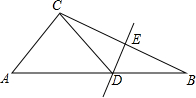 如图,在△ABC中,AC=5,BC=8,BC的中垂线交AB、BC于D、E,DE=3,连CD,当∠ACD=90°时,则AD的长是( )
如图,在△ABC中,AC=5,BC=8,BC的中垂线交AB、BC于D、E,DE=3,连CD,当∠ACD=90°时,则AD的长是( )
 如图,在△ABC中,AC=5,BC=8,BC的中垂线交AB、BC于D、E,DE=3,连CD,当∠ACD=90°时,则AD的长是( )
如图,在△ABC中,AC=5,BC=8,BC的中垂线交AB、BC于D、E,DE=3,连CD,当∠ACD=90°时,则AD的长是( )| A. | 6 | B. | 5$\sqrt{3}$ | C. | 5$\sqrt{2}$ | D. | 8 |
12.在下列各数中,最小的数是( )
| A. | 1 | B. | -1 | C. | -3 | D. | 0 |
 已知在△ABC中,∠BAC=90°,AD⊥BC于点D,点E为AC中点,延长ED、AB交于点F.求证:$\frac{AB}{AC}$=$\frac{DF}{FA}$.
已知在△ABC中,∠BAC=90°,AD⊥BC于点D,点E为AC中点,延长ED、AB交于点F.求证:$\frac{AB}{AC}$=$\frac{DF}{FA}$.