题目内容
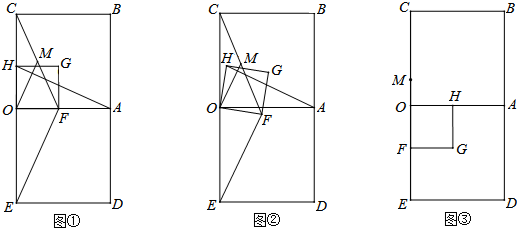
 已知:如图,在Rt△ABC中,∠CAB=90°,AB=AC,D为AC的中点,过点作CF⊥BD交BD的延长线于点F,过点作AE⊥AF于点.
已知:如图,在Rt△ABC中,∠CAB=90°,AB=AC,D为AC的中点,过点作CF⊥BD交BD的延长线于点F,过点作AE⊥AF于点.(1)求证:△ABE≌△ACF;
(2)过点作AH⊥BF于点H,求证:CF=EH.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)利用直角关系得出∠BAE=∠CAF,∠ABD=∠DCF,即可得出△ABE≌△ACF,
(2)由△ABE≌△ACF,得出AE=AF,再由等腰直角三角形得出AH=EH,再证得△ADH≌△CDF即可得出CF=EH
(2)由△ABE≌△ACF,得出AE=AF,再由等腰直角三角形得出AH=EH,再证得△ADH≌△CDF即可得出CF=EH
解答:证明:(1)∵AE⊥AF,∠CAB=90°,
∴∠EAF=∠CAB=90°
∴∠EAF-∠EAC=∠CAB-∠EAC即∠BAE=∠CAF,
∵CF⊥BD,
∴∠BFC=90°=∠CAB,
∴∠BDA+∠ABD=90°,∠DCF+∠FDC=90°,
∵∠ADB=∠FDC,
∴∠ABD=∠DCF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(ASA),
(2)∵由(1)知△ABE≌△ACF,
∴AE=AF,
∵∠EAF=90°,
∴∠AEF=∠AFE=45°,
∵AH⊥BF,
∴∠AHF=∠AHE=90°=∠CFH,
∴∠EAH=180°-∠AHE-∠AEF=45°=∠AEF,
∴AH=EH,
∵D为AC中点,
∴AD=CD,
在△ADH和△CDF中,
,
∴△ADH≌△CDF(AAS),
∴AH=CF,
∴EH=CF.
∴∠EAF=∠CAB=90°
∴∠EAF-∠EAC=∠CAB-∠EAC即∠BAE=∠CAF,
∵CF⊥BD,
∴∠BFC=90°=∠CAB,
∴∠BDA+∠ABD=90°,∠DCF+∠FDC=90°,
∵∠ADB=∠FDC,
∴∠ABD=∠DCF,
在△ABE和△ACF中,
|
∴△ABE≌△ACF(ASA),
(2)∵由(1)知△ABE≌△ACF,
∴AE=AF,
∵∠EAF=90°,
∴∠AEF=∠AFE=45°,
∵AH⊥BF,
∴∠AHF=∠AHE=90°=∠CFH,
∴∠EAH=180°-∠AHE-∠AEF=45°=∠AEF,
∴AH=EH,
∵D为AC中点,
∴AD=CD,
在△ADH和△CDF中,
|
∴△ADH≌△CDF(AAS),
∴AH=CF,
∴EH=CF.
点评:本题主要考查了全等三角形的判定与性质,解题的关键是能根据角和边的关键得出三角形全等.

练习册系列答案
相关题目
 如图,已知AD=CB,AB=CD,AC与BD交于点O,则图中全等三角形共有( )
如图,已知AD=CB,AB=CD,AC与BD交于点O,则图中全等三角形共有( )| A、1对 | B、2对 | C、3对 | D、4对 |
下面四个数中是负数的为( )
| A、0 | ||
| B、3 | ||
| C、-1.2 | ||
D、
|
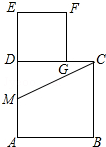 如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为( )
如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为( )A、
| ||
B、3-
| ||
C、
| ||
D、
|
 如图,已知四边形ABCD中,∠A=∠C,∠B=∠D,求证:四边形ABCD是平行四边形.
如图,已知四边形ABCD中,∠A=∠C,∠B=∠D,求证:四边形ABCD是平行四边形.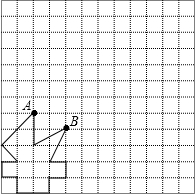 为迎接2014年8月16号在南京举行的青奥会,江都体育迷小强利用网格设计了一个“火炬”图案,请你帮帮他:
为迎接2014年8月16号在南京举行的青奥会,江都体育迷小强利用网格设计了一个“火炬”图案,请你帮帮他: