题目内容
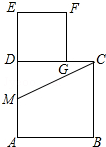如图，在边长为2的正方形ABCD中，M为边AD的中点，延长MD至点E，使ME=MC，以DE为边作正方形DEFG，点G在边CD上，则DG的长为（ ）A、
| ||
B、3-
| ||
C、
| ||
D、
|
考点：勾股定理,正方形的性质
专题：
分析：根据线段中点的定义求出MD，再利用勾股定理列式求出MC，即为ME的长度，然后求出DE，再根据正方形的四条边都相等可得DG=DE．
解答：解：∵正方形ABCD的边长为2，M为边AD的中点，
∴DM=1，MC=
=
，
∵ME=MC，
∴ME=
，
∴DE=
-1，
∵以DE为边作正方形DEFG，点G在边CD上，
∴DG=
-1．
故选：D．
∴DM=1，MC=
| DC2+DM2 |
| 5 |
∵ME=MC，
∴ME=
| 5 |
∴DE=
| 5 |
∵以DE为边作正方形DEFG，点G在边CD上，
∴DG=
| 5 |
故选：D．
点评：本题考查了正方形的性质，勾股定理的应用，线段中点的定义，熟记性质是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如果长、宽、高分别为x、y、z的箱子按如图的方式打包，则打包带的长至少为等腰△ABC的周长为8cm，AB=2cm，则BC的长为（ ）
| A、2cm | B、3cm |
| C、4cm | D、2或3cm |
如果分式
的值为0，那么x的值为（ ）
| x |
| x-2 |
| A、x=2 |
| B、x=0或x=2 |
| C、x=0 |
| D、以上答案都不对 |
如图，?ABCD中，∠B=70°，点E是BC的中点，点F在AB上，且BF=BE，过点F作FG⊥CD于点G，则∠EGC的度数为（ ）| A、35° | B、45° |
| C、30° | D、55° |
已知：如图，在Rt△ABC中，∠CAB=90°，AB=AC，D为AC的中点，过点作CF⊥BD交BD的延长线于点F，过点作AE⊥AF于点．
如图1，在正方形ABCD中，∠ECF的两边分别交边AB、AD于点E、F，且∠ECF=45°．