题目内容
7.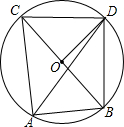 如图,已知点A,点B,点C在圆O上,且BC为圆O的直径,∠CAB的平分线交圆O于点D,若AB=6,AC=8.
如图,已知点A,点B,点C在圆O上,且BC为圆O的直径,∠CAB的平分线交圆O于点D,若AB=6,AC=8.(1)求圆O的半径;
(2)求BD、CD的长.
分析 (1)由圆周角定理可得∠BAC=90°,进而根据勾股定理求出BC的长度,即圆的直径,继而半径可求出;
(2)根据角平分线的定义可得∠DAC=∠BCD,然后求出AD=BD,再根据等腰直角三角形的性质其解即可.
解答 解:(1)∵BC是直径,
∴∠CAB=∠BDC=90°(直径所对的圆周角是直角),
在Rt△ABC中,AB=6,AC=8,
∴BC=10,
∴圆O的半径OC=5;
(2)
∵BC是直径,
∴∠CAB=∠BDC=90°(直径所对的圆周角是直角),
∵∠CAB的平分线交⊙O于点D,
∴∠CAB=∠BAD,
∴$\widehat{CD}=\widehat{BD}$,
∴CD=BD,
∴在Rt△CBD中,CD=BD=$\frac{\sqrt{2}}{2}$×10=5$\sqrt{2}$.
点评 本题考查了勾股定理,圆周角定理,解题的关键是求出∠CAB=∠CDV=90°.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
17.三角形中至少有一个角大于或等于( )
| A. | 30° | B. | 60° | C. | 70° | D. | 80° |
18.下列各式中,y是x的二次函数的是( )
| A. | y=$\frac{1}{x^2}$ | B. | y=x2+x-2 | C. | y=2x+1 | D. | y2=x2+3x |
15.下列各点,在二次函数y=x2-2的图象上的是( )
| A. | (0,0) | B. | (-1,-1) | C. | (1,9) | D. | (2,-2) |
12.把抛物线y=$\frac{1}{2}{x^2}$+1先向右平移1个单位,再向下移2个单位,得到的抛物线解析式是( )
| A. | y=$\frac{1}{2}{({x+1})^2}$-3 | B. | y=$\frac{1}{2}{({x-1})^2}$+3 | C. | y=$\frac{1}{2}{({x+1})^2}$-1 | D. | y=$\frac{1}{2}{({x-1})^2}$-1 |
16.一个数的平方等于这个数的4倍,则这个数是( )
| A. | 0 | B. | 4 | C. | 0或4 | D. | 无法确定 |
 已知:四边形ABCD中,∠B=∠D=90°,∠A=60°,CD=1,AB=$\sqrt{3}$,求BC、AD的长.
已知:四边形ABCD中,∠B=∠D=90°,∠A=60°,CD=1,AB=$\sqrt{3}$,求BC、AD的长.