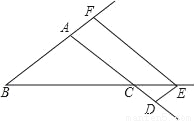
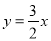题目内容
数学活动课上,小敏、小颖分别画了△ABC和△DEF,数据如图,如果把小敏画的三角形面积记作S△ABC,小颖画的三角形面积记作S△DEF,那么你认为( )
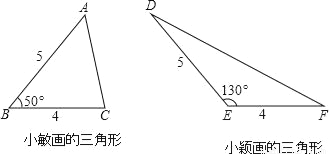
A. S△ABC>S△DEF B. S△ABC<S△DEF C. S△ABC=S△DEF D. 不能确定
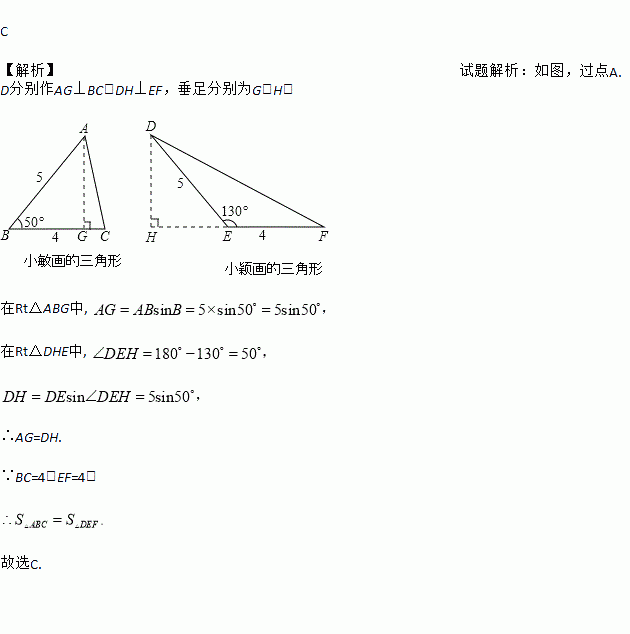
C 【解析】试题解析:如图,过点A.D分别作AG⊥BC,DH⊥EF,垂足分别为G、H, 在Rt△ABG中, 在Rt△DHE中, ∴AG=DH. ∵BC=4,EF=4, 故选C.
练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目

 B.
B.  C.
C.  D.
D. 
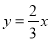 B.
B. 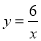 C. y=x D.
C. y=x D.