题目内容
【题目】如图，在
中，
，
,
，点
从点
开始沿
边向点
以
的速度移动，点
从点开始沿
边向
点以
的速度移动.
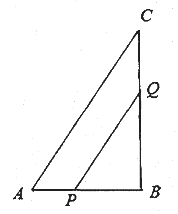
（1）如果点、分别从、同时出发，几秒钟后，
的面积等于
？
（2）在（1）中，的面积能否等于面积的一半？说明理由；
（3）几秒后，点，点相距
？
【答案】（1）经过
或
秒钟，使
的面积为
.（2）的面积不能等于
面积的一半；（3）
秒或秒后，点
，点
相距
.
【解析】
（1）设经过x秒钟，使△PBQ的面积为8cm2，得到BP=6-x，BQ=2x，根据三角形的面积公式得出方程
（6-x）×2x=8，求出即可；
（2）△ABC面积为36cm2，同（1）列方程解答即可；
（3）设t秒后，点P，点Q相距4
cm，依题意得BP=6-t，BQ=2t，利用勾股定理列方程求解．
解：（1）设经过
秒钟，使的面积为，
,
，
，
，
，
，
.
答：经过或秒钟，使的面积为.
（2）由题意得
，
，
，
，
此方程无解，的面积不能等于面积的一半；
（3）设
秒后，点，点相距，由题意得：
，
整理得：
，
解得：
，
，
答：秒或秒后，点，点相距.
练习册系列答案
名校课堂系列答案
相关题目
