Question

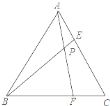
【题目】如图，等边三角形ABC的边长为cm，在AC，BC边上各取一点E，F，使得AE=CF，连接AF，BE相交于点P．（1）则∠APB=______度；（2）当点E从点A运动到点C时，则动点P经过的路径长为________cm.

Answer 1

【答案】120

【解析】

（1）证明△ABE≌△CAF，借用外角即可以得到答案；

（2）由∠APB＝120°可知点P的运动路径是一段弧，根据圆周角定理可得∠AOB＝120°，过圆心O做OG⊥AB，由AB＝可得OA＝1，然后利用弧长公式计算即可.

解：（1）∵△ABC为等边三角形，

∴AB＝AC，∠C＝∠CAB＝60°，

又∵AE＝CF，

在△ABE和△CAF中，，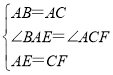

∴△ABE≌△CAF（SAS），

∴∠ABE＝∠CAF，

又∵∠APE＝∠BPF＝∠ABP＋∠BAP，

∴∠APE＝∠BAP＋∠CAF＝60°，

∴∠APB＝180°∠APE＝120°；

（2）由∠APB＝120°可知点P的运动路径是一段弧，如图，

∵∠APB＝120°，

所以劣弧AB所对的圆周角为60°，

∴∠AOB＝120°，

过圆心O做OG⊥AB，则∠AOG=30°，

又∵AB＝，

∴AG＝，

∴OA＝，

∴动点P经过的路径长l＝．

故答案为：（1）120；（2）.