题目内容
14.解方程组:$\left\{\begin{array}{l}{\frac{6}{x-y}+\frac{4}{x+y}=3}\\{\frac{9}{x-y}-\frac{1}{x+y}=1}\end{array}\right.$.分析 利用换元法,设$\frac{1}{x-y}$=a,$\frac{1}{x+y}$=b,转化为关于a、b的方程组即可解决问题.
解答 解:设$\frac{1}{x-y}$=a,$\frac{1}{x+y}$=b,
则有$\left\{\begin{array}{l}{6a+4b=3}\\{9a-b=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{1}{6}}\\{b=\frac{1}{2}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x-y=6}\\{x+y=2}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=4}\\{y=-2}\end{array}\right.$.
点评 本题考查方程组的解,解题的关键是学会利用换元法解决问题,学会用转化的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
5.如果水位下降3m,记作+3m,那么水位上升4m,记作( )
| A. | 1m | B. | 7m | C. | 4m | D. | -4m |
19.解关于x的方程-3x-9=$\frac{1}{2}$x+5,下面的变形正确的是( )
| A. | -3x+$\frac{1}{2}$x=5-9 | B. | -3x-$\frac{1}{2}$x=(-9)+(-5) | C. | $\frac{1}{2}$x+3x=(-9)+(-5) | D. | $\frac{1}{2}$x+3x=5+9 |
 如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.请完整填上结论或依据.
如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.请完整填上结论或依据.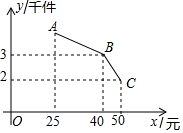 今年是“精准扶贫”攻坚关键年,某扶贫工作队为对口扶贫村引进建立了一村集体企业,并无偿提供一笔无息贷款作为启动资金,双方约定:①企业生产出的产品全部由扶贫工作队既是联系商家收购;②企业从生产销售的利润中,要保证按时发放工人每月最低工资32000元.已知该企业生产的产品成本为20元/件,月生产量y(千件)与出厂价x(元)(25≤x≤50)的函数关系可用图中的线段AB和BC表示,其中AB的解析式为y=-$\frac{1}{20}$x+m(m为常数).
今年是“精准扶贫”攻坚关键年,某扶贫工作队为对口扶贫村引进建立了一村集体企业,并无偿提供一笔无息贷款作为启动资金,双方约定:①企业生产出的产品全部由扶贫工作队既是联系商家收购;②企业从生产销售的利润中,要保证按时发放工人每月最低工资32000元.已知该企业生产的产品成本为20元/件,月生产量y(千件)与出厂价x(元)(25≤x≤50)的函数关系可用图中的线段AB和BC表示,其中AB的解析式为y=-$\frac{1}{20}$x+m(m为常数). 如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37°,求∠D的度数.
如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37°,求∠D的度数.