Question

如图，在由边长为1的25个小正方形组成的正方形网格上有一个△ABC，在这个网格上画一个与△ABC相似，且面积最大的△A₁B₁C₁（A₁，B₁，C₁，三点都在格点上）．则这个三角形的面积是______．

Answer 1

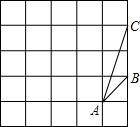
利用勾股定理得出△ABC各边长AB=

2

，BC=2，AC=

10

，
故AC的对应边A₁C₁最长的长度为

5

×

10

=

50

=5

2

，A₁C₁=5

2

，A₁B₁=

10

，B₁C₁=2

5

．
∵

A1C1

AC

=

50

10

=

5

，
∴

S△A1B1C1

S△ABC

=

(A1C1)2

(AC)2

=5，
∵S_△ABC=

1

2

×1×2=1，
∴△A₁B₁C₁的面积为：5．