题目内容
如图，在梯形ABCD中，AB∥CD，AD⊥AB，AB=3，CD=2，AD=7，试问在AD上是否存在点P，使得以A，B，P为顶点的三角形与△DCP是相似三角形？如果不存在，请说明理由；如果存在这样的点有几个？它距A点多远？
在AD上是否存在点P，使得以A，B，P为顶点的三角形与△DCP是相似三角形，
理由如下：
设P为AD上一点，且PA=x，
若△DCP∽△APB或△DCP∽△ABP，则，
=
或
=
，
∵AB=3，CD=2，AD=7，
∴
=
或
=
，
∴x2-7x+6=0或2x=21-3x，
解得：x=1或6或
，
∴在AD上存在点P，使得以A、B、P为顶点的三角形与△DCP相似，这样的点P有三个，它距A点分别为 1，6，
．
理由如下：
设P为AD上一点，且PA=x，
若△DCP∽△APB或△DCP∽△ABP，则，
| CD |
| PA |
| DP |
| AB |
| CD |
| AB |
| DP |
| AP |
∵AB=3，CD=2，AD=7，
∴
| 2 |
| x |
| 7-x |
| 3 |
| 2 |
| 3 |
| 7-x |
| x |
∴x2-7x+6=0或2x=21-3x，
解得：x=1或6或
| 21 |
| 5 |
∴在AD上存在点P，使得以A、B、P为顶点的三角形与△DCP相似，这样的点P有三个，它距A点分别为 1，6，
| 21 |
| 5 |
练习册系列答案
相关题目
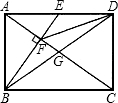
线EF折叠，使D与C重合，CE与CF分别交AB于点G、H．