题目内容
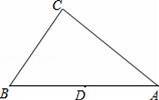
如图,△ABC中,AB=5,BC=3,CA=4,D为AB的中点,过点D的直线与BC交于点E,若直线DE截△ABC所得的三角形与△ABC相似,则DE= .

2或
 .
.
【考点】相似三角形的判定.
【专题】计算题.
【分析】当直线DE截△ABC所得的△BDE与△ABC相似,如图1,则
 =
=
 ,利用比例性质可计算出DE;当直线DE截△ABC所得的△ADF与△ABC相似,如图2,易证得△BDE∽△BCA,则
,利用比例性质可计算出DE;当直线DE截△ABC所得的△ADF与△ABC相似,如图2,易证得△BDE∽△BCA,则
 =
=
 ,然后利用比例性质可求出DE.
,然后利用比例性质可求出DE.
【解答】解:∵D为AB的中点,
∴BD=
 AB=
AB=
 ,
,
∵∠DBE=∠ABC,
∴当∠DBE=∠ACB时,△BDE∽△BAC时,如图1,则
 =
=
 ,即
,即
 =
=
 ,解得DE=2;
,解得DE=2;


当∠BDE=∠ACB时,如图2,DE交AC于F,


∵∠DAF=∠CAB,
∴△ADF∽△ACB,
∴△BDE∽△BCA,
∴
 =
=
 ,即
,即
 =
=
 ,解得DE=
,解得DE=
 ,
,
综上所述,若直线DE截△ABC所得的三角形与△ABC相似,则DE=2或
 .
.
故答案为2或
 .
.
【点评】本题考查了相似三角形判定:有两组角对应相等的两个三角形相似.也考查了相似三角形的性质.注意分类讨论思想的运用.

练习册系列答案
相关题目
 m耗油量为0.5升,则从出发到收工共
m耗油量为0.5升,则从出发到收工共 耗油多少升?
耗油多少升?
 |+(cosB﹣
|+(cosB﹣

 有意义的x的取值范围是 .
有意义的x的取值范围是 .
 +
+
 =2;
=2; 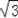
 ,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1,连接A1B1,再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 .
,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1,连接A1B1,再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 .