题目内容
7. 如图,点E是矩形ABCD的边AD的中点,点P是边BC上的动点,PM⊥BE,PN⊥CE,垂足分别是M、N.
如图,点E是矩形ABCD的边AD的中点,点P是边BC上的动点,PM⊥BE,PN⊥CE,垂足分别是M、N.求:当AB和AD应满足怎样的数量关系时,四边形PMEN是矩形?请说明理由.
分析 由SAS证明△ABE≌△DCE,得出∠AEB=∠DEC,由矩形的性质得出∠BEC=90°,得出∠AEB=∠DEC=45°证出AE=DE=DC,即AD=2AB.
解答 解:当AD=2AB时.四边形PMEN为矩形;理由如下:
∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=DC,
又∵点E是矩形ABCD的边AD的中点.
∴AE=DE,
在△ABE和△CDE中,$\left\{\begin{array}{l}{AE=DE}\\{∠A=∠D}\\{AB=DC}\end{array}\right.$,
∴△ABE≌△DCE(SAS),
∴∠AEB=∠DEC,
∵四边形PMEN为矩形,
∴∠BEC=90°,
∴∠AEB=∠DEC=45°
∴AE=DE=DC,即AD=2AB.
∴当AD=2AB时;四边形PMEN为矩形.
点评 本题考查了矩形的判定与性质、全等三角形的判定与性质、正方形的判定与性质;熟练掌握矩形的判定与性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
2.下列各式中正确的是( )
| A. | $\overrightarrow{a}$+(-$\overrightarrow{a}$)=0 | B. | $\overrightarrow{a}$+$\overrightarrow{0}$=-$\overrightarrow{a}$ | C. | $\overrightarrow{0}$+(-$\overrightarrow{a}$)=$\overrightarrow{a}$ | D. | |$\overrightarrow{0}$|=0 |
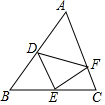 如图,设△ABC的面积为1,点D,E,F分别在AB,BC,CA上,AD=$\frac{1}{m}$AB,BE=$\frac{1}{n}$BC,CF=$\frac{1}{p}$CA,且满足m+n+p=9,m2+n2+p2=29.m3+n3+p3=99,求△DEF的面积.
如图,设△ABC的面积为1,点D,E,F分别在AB,BC,CA上,AD=$\frac{1}{m}$AB,BE=$\frac{1}{n}$BC,CF=$\frac{1}{p}$CA,且满足m+n+p=9,m2+n2+p2=29.m3+n3+p3=99,求△DEF的面积.



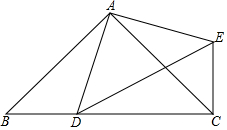 填空:把下面的推里过程补充完整,并在括号内注明理由.
填空:把下面的推里过程补充完整,并在括号内注明理由. 如图,一个碗的高度为7cm,两个碗摞在一起后高度为7.8cm.
如图,一个碗的高度为7cm,两个碗摞在一起后高度为7.8cm.