题目内容
17.先化简,再求值:$({\frac{3x+4}{{{x^2}-1}}-\frac{2}{x-1}})÷\frac{x+2}{{{x^2}-2x+1}}$,其中x从-1、+1、-2-3中选出你认为合理的数代入化简后的式子中求值.分析 先把括号内通分后进行同分母的减法运算,再把分子分母因式分解和把除法运算化为乘法运算,然后约分后得到原式=$\frac{x-1}{x+1}$,根据分式有意义的条件,把x=-3代入计算即可.
解答 解:原式=$[{\frac{3x+4}{(x+1)(x-1)}-\frac{2(x+1)}{(x+1)(x-1)}}]÷\frac{x+2}{{{{(x-1)}^2}}}$
=$\frac{3x+4-2x-2}{(x+1)(x-1)}÷\frac{x+2}{{{{(x-1)}^2}}}$
=$\frac{x+2}{(x+1)(x-1)}•\frac{{{{(x-1)}^2}}}{x+2}$
=$\frac{x-1}{x+1}$,
当x=-3时,原式=$\frac{-3-1}{-3+1}$=2.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
5.下列式子不正确的是( )
| A. | ${2^{-1}}=\frac{1}{2}$ | B. | (-2)-2=4 | C. | ${({\frac{1}{2}})^{-3}}$=8 | D. | (-2)0=1 |
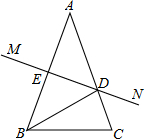 如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.若∠DBC=33°,∠A的度数为38°.
如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.若∠DBC=33°,∠A的度数为38°.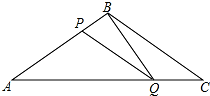 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒. 如图,在△ABC中,∠BAC=90°,AB=AC,BE平分∠ABC,交AC于点D,延长BA至点F,连接CF,且BE⊥CF.
如图,在△ABC中,∠BAC=90°,AB=AC,BE平分∠ABC,交AC于点D,延长BA至点F,连接CF,且BE⊥CF.