题目内容
16.四边形ABCD是菱形,∠ABC=120°,AB=12cm,则∠ABD的度数为60°,∠DAB的度数为60°;对角线BD=12cm,AC=12$\sqrt{3}$cm;菱形ABCD的面积为72$\sqrt{3}$cm2.分析 由菱形的性质:对角线互相平分每一组对角可求出∠ABD的度数;邻角互补可求出∠DAB的度数;利用勾股定理可求出AO,BO的长进而可求出对角线AC,BD的长,由菱形的面积公式再求出其面积即可.
解答  解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,
∴BD平分∠ABC,∠DAB+∠ABC=180°,
∵∠ABC=120°,
∴∠ABD=60°,∠DAB=60°,
∴∠BAO=30°
∵AB=12cm,
∴BO=6cm,
∴AO=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$,
∴BD=12cm,AC=12$\sqrt{3}$,
∴菱形ABCD的面积=$\frac{1}{2}$×12×12$\sqrt{3}$=72$\sqrt{3}$cm2,
故答案为:60°,60°,12cm,12$\sqrt{3}$cm,72$\sqrt{3}$cm2.
点评 本题考查了菱形的性质以及菱形面积的计算,解题的关键是熟记菱形的各种性质:①菱形具有平行四边形的一切性质;②菱形的四条边都相等; ③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
4.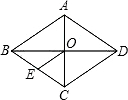 已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )
已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )
 已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )
已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )| A. | 6cm | B. | 5cm | C. | 4cm | D. | 3cm |
6. 如图,△ABC≌△CDA,并且AB=CD,那么下列结论错误的是( )
如图,△ABC≌△CDA,并且AB=CD,那么下列结论错误的是( )
 如图,△ABC≌△CDA,并且AB=CD,那么下列结论错误的是( )
如图,△ABC≌△CDA,并且AB=CD,那么下列结论错误的是( )| A. | ∠1=∠2 | B. | AC=CA | C. | AC=BC | D. | ∠D=∠B |
 如图都是小方格,A,B,C构成三角形,则cosA=$\frac{3}{5}$.
如图都是小方格,A,B,C构成三角形,则cosA=$\frac{3}{5}$.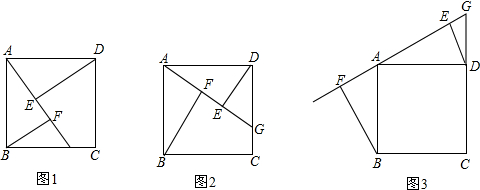
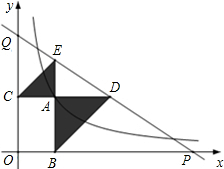 如图,已知动点A在函数y=$\frac{4}{x}$(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于$\frac{68}{15}$.
如图,已知动点A在函数y=$\frac{4}{x}$(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于$\frac{68}{15}$.