题目内容
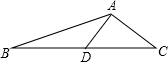如图，∠BAC=120°，AD⊥AC，BD=CD，则下列结论正确的是（ ）| A、AD=AC | ||
B、AB=
| ||
| C、AB=2AC | ||
D、AB=
|
分析：由题意作图延长AD到E，使DE=AD，连接BE、CE，证明四边形ABEC是平行四边形，AB=CE，在直角△ACE中即可对四个选项求解作出判断．
解答：解：延长AD到E，使DE=AD，连接BE、CE，
则四边形ABEC是平行四边形，
∵∠BAC=120°，AD⊥AC，BD=CD
∴∠AEC=30°
则A中
=
=
×cot30°=
，故本选项错误；
B中
=
=2，故本选项错误；
C中
=
=2，故本选项正确；
D中
=
=2，故本选项错误．
故选C．
则四边形ABEC是平行四边形，
∵∠BAC=120°，AD⊥AC，BD=CD
∴∠AEC=30°
则A中
| AD |
| AC |
| ||
| AC |
| 1 |
| 2 |
| ||
| 2 |
B中
| AB |
| AC |
| EC |
| AC |
C中
| AB |
| AC |
| EC |
| AC |
D中
| AB |
| AC |
| EC |
| AC |
故选C．
点评：本题考查了含30度角的直角三角形，本题从每个选项中假设成立来论证．
练习册系列答案
相关题目
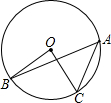如图，已知圆心角∠AOC=78°，则圆周角∠BAC的度数是（ ）| A、156° | B、78° | C、39° | D、12° |
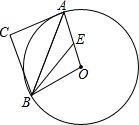（2013•十堰模拟）如图，Rt△ABC中，∠ACB=90°，BC=4，AC=3，点A、B在圆O上，且∠BAC=
，那么AD=_________________.
