题目内容
如图28-1-12所示，在△ABC中，∠C=90°，∠B=30°，AD是∠BAC的平分线，已知AB=
，那么AD=_________________.
答案：
解析：
解析：
|
思路解析：在Rt△ABC中，利用30°角和斜边长求直角边AC长，再由角平分线可求Rt△ACD中特殊角30°（或60°），由正余弦函数关系式求出AD长.
此题的方法不唯一，也可结合勾股定理求得，但方法较麻烦，所以做题时应仔细考虑特殊角所在的直角三角形，用哪个函数关系可求哪条边. ∵在Rt△ABC中，∠C=90°，∠B=30°，AB=43， ∴AC=ABsinB= 又∵AD是∠BAC的平分线，∴∠CAD= ∴在Rt△ACD中，AD= 答案：4 |
sin30°=
.
∠CAB=
.
练习册系列答案
相关题目
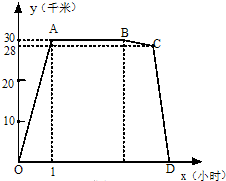23、周六上午8：O0小明从家出发，乘车1小时到郊外某基地参加社会实践活动，在基地活动2.2小时后，因家里有急事，他立即按原路以4千米/时的平均速度步行返回．同时爸爸开车从家出发沿同一路线接他，在离家28千米处与小明相遇．接到小明后保持车速不变，立即按原路返回．设小明离开家的时间为x小时，小明离家的路程y（干米）与x（小时）之间的函致图象如图所示，
如图所示，线段AB上一点C，点D是线段BC的中点，已知AB=28，AC=12，则AD=（ ）| A、16 | B、18 | C、20 | D、22 |
