题目内容
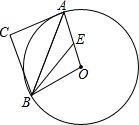 (2013•十堰模拟)如图,Rt△ABC中,∠ACB=90°,BC=4,AC=3,点A、B在圆O上,且∠BAC=
(2013•十堰模拟)如图,Rt△ABC中,∠ACB=90°,BC=4,AC=3,点A、B在圆O上,且∠BAC=| 1 |
| 2 |
(1)求证:直线AC是⊙O的切线;
(2)求⊙O半径的长;
(3)求
| AE |
| AO |
分析:(1)过点O作OF⊥AB于F,根据垂径定理可得∠AOF=
∠AOB,从而得到∠BAC=∠AOF,然后求出∠OAC=∠OAF+∠AOF=90°,再根据切线的定义证明即可;
(2)利用勾股定理列式求出AB的长,然后求出△ABC和△AOF相似,利用相似三角形对应边成比例列式求解即可得解;
(3)根据角平分线的性质可得
=
,然后求解即可.
| 1 |
| 2 |
(2)利用勾股定理列式求出AB的长,然后求出△ABC和△AOF相似,利用相似三角形对应边成比例列式求解即可得解;
(3)根据角平分线的性质可得
| AE |
| OE |
| AB |
| OB |
解答:(1)证明:如图,过点O作OF⊥AB于F,
由垂径定理得,∠AOF=
∠AOB,
∵∠BAC=
∠AOB,
∴∠BAC=∠AOF,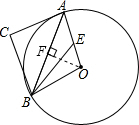
∴∠BAC+∠OAF=∠AOF+∠OAF=180°-90°=90°,
∴OA⊥AC,
∵点A在⊙O上,
∴直线AC是⊙O的切线;
(2)解:∵∠ACB=90°,BC=4,AC=3,
∴AB=
=
=5,
∴AF=
AB=
,
∵∠BAC=∠AOF,∠ACB=∠AFO=90°,
∴△ABC∽△AOF,
∴
=
,
即
=
,
解得AO=
,
即,⊙O半径的长
;
(3)解:∵BE是∠ABO的平分线,
∴
=
=
=
,
∴
=
=
.
由垂径定理得,∠AOF=
| 1 |
| 2 |
∵∠BAC=
| 1 |
| 2 |
∴∠BAC=∠AOF,

∴∠BAC+∠OAF=∠AOF+∠OAF=180°-90°=90°,
∴OA⊥AC,
∵点A在⊙O上,
∴直线AC是⊙O的切线;
(2)解:∵∠ACB=90°,BC=4,AC=3,
∴AB=
| AC2+BC2 |
| 32+42 |
∴AF=
| 1 |
| 2 |
| 5 |
| 2 |
∵∠BAC=∠AOF,∠ACB=∠AFO=90°,
∴△ABC∽△AOF,
∴
| AO |
| AB |
| AF |
| BC |
即
| AO |
| 5 |
| ||
| 4 |
解得AO=
| 25 |
| 8 |
即,⊙O半径的长
| 25 |
| 8 |
(3)解:∵BE是∠ABO的平分线,
∴
| AE |
| OE |
| AB |
| OB |
| 5 | ||
|
| 8 |
| 5 |
∴
| AE |
| AO |
| 8 |
| 5+8 |
| 8 |
| 13 |
点评:本题是圆的综合题型,主要考查了圆的切线的定义,勾股定理的应用,相似三角形的判定与性质,角平分线的性质,(3)角平分线分对边所成的两条线段的比等于两边的比大部分教材已经不作要求,可酌情使用.

练习册系列答案
相关题目
 (2013•十堰模拟)如图是用火柴棍摆成的边长分别是1,2,3根火柴棍时的正方形,所用的火柴根数分别为4,12,24,按此摆法,当边长为6根火柴棍时,所用的火柴根数为( )
(2013•十堰模拟)如图是用火柴棍摆成的边长分别是1,2,3根火柴棍时的正方形,所用的火柴根数分别为4,12,24,按此摆法,当边长为6根火柴棍时,所用的火柴根数为( ) (2013•十堰模拟)矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,则折痕EF长度是( )
(2013•十堰模拟)矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,则折痕EF长度是( ) (2013•十堰模拟)如图已知二次函数y=ax2+bx+c的图象与y轴正半轴相交,对称轴为直线x=1,顶点坐标P(1,4).则下列结论中:
(2013•十堰模拟)如图已知二次函数y=ax2+bx+c的图象与y轴正半轴相交,对称轴为直线x=1,顶点坐标P(1,4).则下列结论中: