题目内容
18.解下列方程(1)x2+2x=1
(2)(x-3)2+2(x-3)=0
(3)-3x2+4x+1=0.
分析 (1)先配方,开方,即可得出两个一元一次方程,求出方程的解即可;
(2)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(3)方程两边都除以-1,再求出b2-4ac的值,最后代入公式求出即可.
解答 解:(1)x2+2x=1,
x2+2x+1=2,
(x+1)2=2,
x+1=$±\sqrt{2}$,
x1=-1+$\sqrt{2}$,x2=-1-$\sqrt{2}$;
(2)(x-3)2+2(x-3)=0,
(x-3)(x-3+2)=0,
x-3=0,x-3+2=0,
x1=3,x2=1;
(3)-3x2+4x+1=0,
3x2-4x-1=0,
b2-4ac=(-4)2-4×3×(-1)=28,
x=$\frac{4±\sqrt{28}}{2×3}$,
x1=$\frac{2+\sqrt{7}}{3}$,x2=$\frac{2-\sqrt{7}}{3}$.
点评 本题考查了解一元二次方程的应用,能选择适当的方法解一元二次方程是解此题的关键.

练习册系列答案
相关题目
7.设⊙O的半径为r,若点P在直线a上,且OP=r,则直线a与⊙O的位置关系为( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 相交或相切 |
 如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则tan∠AED=$\frac{1}{2}$.
如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则tan∠AED=$\frac{1}{2}$.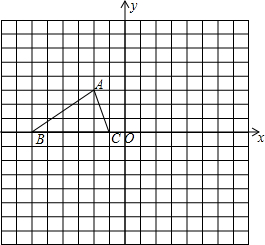 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).