题目内容
4.当-7≤x≤a时,二次函数y=-$\frac{1}{2}$(x+3)2+5恰好有最大值3,则a=-5.分析 根据抛物线解析式得到顶点坐标(-3,5);然后由抛物线的增减性进行解答.
解答 解:∵y=-$\frac{1}{2}$(x+3)2+5,
∴该抛物线的开口方向向下,且顶点坐标是(-3,5).
∴当x<-3时,y随x的增大而增大,
∴当x=a时,二次函数y=-$\frac{1}{2}$(x+3)2+5恰好有最大值3,
把y=3代入函数解析式得到 3=-$\frac{1}{2}$(x+3)2+5,
解得 x1=-5,x2=-1.
∴a=-5.
故答案是:-5.
点评 本题考查了二次函数的最值.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
12. 如图,关于抛物线y=x2+2x-1,下列说法错误的是( )
如图,关于抛物线y=x2+2x-1,下列说法错误的是( )
 如图,关于抛物线y=x2+2x-1,下列说法错误的是( )
如图,关于抛物线y=x2+2x-1,下列说法错误的是( )| A. | 顶点坐标为(-1,-2) | B. | 对称轴是直线x=-l | ||
| C. | 开口方向向上 | D. | 当x>-1时,y随x的增大而减小 |
19.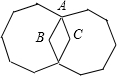 如图,平面上有两个全等的正八边形,∠BAC为( )
如图,平面上有两个全等的正八边形,∠BAC为( )
 如图,平面上有两个全等的正八边形,∠BAC为( )
如图,平面上有两个全等的正八边形,∠BAC为( )| A. | 60° | B. | 45° | C. | 30° | D. | 72° |
9. 如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则边C1D1的长是( )
如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则边C1D1的长是( )
 如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则边C1D1的长是( )
如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则边C1D1的长是( )| A. | 10 | B. | 12 | C. | $\frac{45}{4}$ | D. | $\frac{36}{5}$ |
13.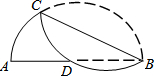 将弧BC沿弦BC折叠,交直径AB于点D,若AD=8,DB=10,则BC的长是( )
将弧BC沿弦BC折叠,交直径AB于点D,若AD=8,DB=10,则BC的长是( )
 将弧BC沿弦BC折叠,交直径AB于点D,若AD=8,DB=10,则BC的长是( )
将弧BC沿弦BC折叠,交直径AB于点D,若AD=8,DB=10,则BC的长是( )| A. | 6$\sqrt{7}$ | B. | 16 | C. | 2$\sqrt{65}$ | D. | 4$\sqrt{15}$ |
 如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图和左视图的面积之和是5.
如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图和左视图的面积之和是5.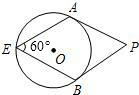 如图,点E是半径为6的⊙O上一点,过点E作一只60°的圆周角∠AEB,分别过点A、B作⊙O的切线,两条切线交于点P.那么四边形AEBP的面积的最大值是54$\sqrt{3}$.
如图,点E是半径为6的⊙O上一点,过点E作一只60°的圆周角∠AEB,分别过点A、B作⊙O的切线,两条切线交于点P.那么四边形AEBP的面积的最大值是54$\sqrt{3}$.