题目内容
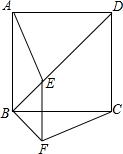 如图,在正方形ABCD中,点E是对角线BD上任意一点,连接AE,将△ABE顺时针旋转90°得到△CBF,连接EF,请判断线段EF与BC之间的位置关系,并说明理由.
如图,在正方形ABCD中,点E是对角线BD上任意一点,连接AE,将△ABE顺时针旋转90°得到△CBF,连接EF,请判断线段EF与BC之间的位置关系,并说明理由.考点:旋转的性质,正方形的性质
专题:探究型
分析:根据正方形的性质得到∠DBC=45°,再根据旋转的性质得到∠EBF=90°,BE=BF,可计算出∠FBC=90°-45°=45°,则BC为等腰直角三角形EBF的顶角的平分线,根据等腰三角形的性质即可得到
BC垂直平分EF.
BC垂直平分EF.
解答:解:BC垂直平分EF.理由如下:
∵四边形ABCD为正方形,
∴∠DBC=45°,
∴将△ABE顺时针旋转90°可得到△CBF,
∴∠EBF=90°,BE=BF,
∴∠FBC=90°-45°=45°,
∴BC为等腰直角三角形EBF的顶角的平分线,
∴BC垂直平分EF.
∵四边形ABCD为正方形,
∴∠DBC=45°,
∴将△ABE顺时针旋转90°可得到△CBF,
∴∠EBF=90°,BE=BF,
∴∠FBC=90°-45°=45°,
∴BC为等腰直角三角形EBF的顶角的平分线,
∴BC垂直平分EF.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了正方形的性质和等腰三角形的性质.

练习册系列答案
相关题目
在平面直角坐标系中,点P(a,b)满足a•b<0,则点P在( )
| A、第二象限 |
| B、第三象限 |
| C、第一象限或第三象限 |
| D、第二象限或第四象限 |
某校租用三辆汽车组织学生去参加中考体育测试,其中小明和王老师都可以从这三辆车中任选一辆搭乘.则小明和王老师同乘一辆车的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|

 如图,半径为12的⊙O中,弦AB与弦CD垂直相交于点E,若AB=16
如图,半径为12的⊙O中,弦AB与弦CD垂直相交于点E,若AB=16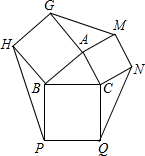 如图,对于任意△ABC,分别以它的三边为边长作一个正方形.求证:S△AGM+S△BHP+S△CNQ=3S△ABC.
如图,对于任意△ABC,分别以它的三边为边长作一个正方形.求证:S△AGM+S△BHP+S△CNQ=3S△ABC.