题目内容
 如图,半径为12的⊙O中,弦AB与弦CD垂直相交于点E,若AB=16
如图,半径为12的⊙O中,弦AB与弦CD垂直相交于点E,若AB=16| 2 |
| 15 |
考点:垂径定理,勾股定理
专题:计算题
分析:过O作OM垂直于AB,ON垂直于CD,利用垂径定理得到M与N分别为AB、CD的中点,求出AM与DN的长,在直角三角形AOM中,利用勾股定理求出OM的长,即为EN的长,在直角三角形ODN中,利用勾股定理求出ON的长,在直角三角形AEN中,利用勾股定理即可求出OE的长.
解答: 解:过O作OM⊥AB,ON⊥CD,连接OA,OD,
解:过O作OM⊥AB,ON⊥CD,连接OA,OD,
∴M为AB的中点,N为CD的中点,四边形MONE为矩形,
∵AB=16
,CD=6
,
∴AM=BM=8
,CN=ND=3
,
又∵OA=OD=12,
∴OM=EN=
=6,ON=
=3,
在Rt△OEN中,利用勾股定理得:OE=
=3
.
故答案为:3
 解:过O作OM⊥AB,ON⊥CD,连接OA,OD,
解:过O作OM⊥AB,ON⊥CD,连接OA,OD,∴M为AB的中点,N为CD的中点,四边形MONE为矩形,
∵AB=16
| 2 |
| 15 |
∴AM=BM=8
| 2 |
| 15 |
又∵OA=OD=12,
∴OM=EN=
| OA2-AM2 |
| OD2-DN2 |
在Rt△OEN中,利用勾股定理得:OE=
| ON2+EN2 |
| 5 |
故答案为:3
| 5 |
点评:此题考查了垂径定理,勾股定理,以及矩形的判定与性质,熟练掌握定理是解本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
一组数据1,2,x,6的众数是2,则x的值是( )
| A、1 | B、2 | C、4 | D、6 |
a3+a3等( )
| A、a6 |
| B、2a3 |
| C、2a6 |
| D、a3 |
估算
-3的值在( )
| 27 |
| A、1与2之间 |
| B、2与3之间 |
| C、3与4之间 |
| D、5与6之间 |
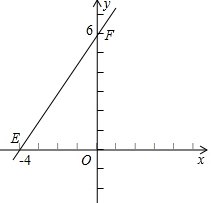 如图,直线l:y=kx+6分别于x轴,y轴交于E、F点,点E的坐标为(-4,0).若点A的坐标为(-3,0),点P(x,y)是平面内的一个动点.
如图,直线l:y=kx+6分别于x轴,y轴交于E、F点,点E的坐标为(-4,0).若点A的坐标为(-3,0),点P(x,y)是平面内的一个动点.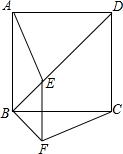 如图,在正方形ABCD中,点E是对角线BD上任意一点,连接AE,将△ABE顺时针旋转90°得到△CBF,连接EF,请判断线段EF与BC之间的位置关系,并说明理由.
如图,在正方形ABCD中,点E是对角线BD上任意一点,连接AE,将△ABE顺时针旋转90°得到△CBF,连接EF,请判断线段EF与BC之间的位置关系,并说明理由. 实践操作:
实践操作: 如图,已知点P是半径为r的圆的圆心.
如图,已知点P是半径为r的圆的圆心.