题目内容
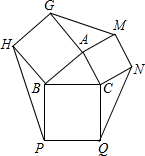 如图,对于任意△ABC,分别以它的三边为边长作一个正方形.求证:S△AGM+S△BHP+S△CNQ=3S△ABC.
如图,对于任意△ABC,分别以它的三边为边长作一个正方形.求证:S△AGM+S△BHP+S△CNQ=3S△ABC.考点:正方形的性质,全等三角形的判定与性质
专题:证明题
分析:可以利用正方形的性质和平移的性质,把△AEF沿AB平移,△HCG沿CB方向平移,使A、C重合于B,F、G重合于I,通过证明三角形全等,且可得∠EAF+∠GCH+∠DBK=360°,然后再证明S△DIK=3S△ABC,就可以得出结论.
解答: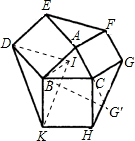 证明:把△AEF沿AB平移,△HCG沿CB方向平移,
证明:把△AEF沿AB平移,△HCG沿CB方向平移,
使A、C重合于B,F、G重合于I,连接DI,BI,KI,
∴△DBI≌△AEF,△BIK≌△HCG,
∵∠EAF+∠BAC+∠ABC+∠GCH+∠ACB+∠DBK=540°,且∠BAC+∠ABC+∠ACB=180°
∴∠EAF+∠GCH+∠DBK=360°,
∴可拼成一个△DIK,
把△GCH绕C点旋转90°,得到△BCG′,
∵∠ACB+∠GCH=180°,
∴∠ACB+∠BCG′=180°
∴A,C,G′在一条直线上,且C为AG′的中点.
∴S△BCG′=S△ABC,
∴S△BIK=S△ABC,
同理S△DBK=S△DBI=S△ABC,
∴由DK、EF、GH为三边构成的△DIK的面积S△DIK=3S△ABC.
∴S△AGM+S△BHP+S△CNQ=3S△ABC.
 证明:把△AEF沿AB平移,△HCG沿CB方向平移,
证明:把△AEF沿AB平移,△HCG沿CB方向平移,使A、C重合于B,F、G重合于I,连接DI,BI,KI,
∴△DBI≌△AEF,△BIK≌△HCG,
∵∠EAF+∠BAC+∠ABC+∠GCH+∠ACB+∠DBK=540°,且∠BAC+∠ABC+∠ACB=180°
∴∠EAF+∠GCH+∠DBK=360°,
∴可拼成一个△DIK,
把△GCH绕C点旋转90°,得到△BCG′,
∵∠ACB+∠GCH=180°,
∴∠ACB+∠BCG′=180°
∴A,C,G′在一条直线上,且C为AG′的中点.
∴S△BCG′=S△ABC,
∴S△BIK=S△ABC,
同理S△DBK=S△DBI=S△ABC,
∴由DK、EF、GH为三边构成的△DIK的面积S△DIK=3S△ABC.
∴S△AGM+S△BHP+S△CNQ=3S△ABC.
点评:本题考查了正方形的性质的运用,三角形全等的判定与性质的运用,图形的旋转和平移的运用,邻补角的性质的运用,解答时运用图形的旋转和平移是解答问题的关键.

练习册系列答案
相关题目
a3+a3等( )
| A、a6 |
| B、2a3 |
| C、2a6 |
| D、a3 |
估算
-3的值在( )
| 27 |
| A、1与2之间 |
| B、2与3之间 |
| C、3与4之间 |
| D、5与6之间 |
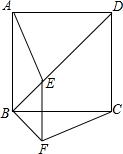 如图,在正方形ABCD中,点E是对角线BD上任意一点,连接AE,将△ABE顺时针旋转90°得到△CBF,连接EF,请判断线段EF与BC之间的位置关系,并说明理由.
如图,在正方形ABCD中,点E是对角线BD上任意一点,连接AE,将△ABE顺时针旋转90°得到△CBF,连接EF,请判断线段EF与BC之间的位置关系,并说明理由.
 如图,边长为2的等边△ABP置于边长为4的正方形AXYZ内,使点B在边AX上.将三角形先绕点B作顺时针旋转,然后再绕P作顺时针旋转,如此进行,使三角形沿着正方形的边向前转动,直到P回到原来位置.这时顶点P所行路程长度为
如图,边长为2的等边△ABP置于边长为4的正方形AXYZ内,使点B在边AX上.将三角形先绕点B作顺时针旋转,然后再绕P作顺时针旋转,如此进行,使三角形沿着正方形的边向前转动,直到P回到原来位置.这时顶点P所行路程长度为