题目内容
19.定义:若四边形中某个顶点与其它三个顶点的距离相等,则这个四边形叫做等距四边形,这个顶点叫做这个四边形的等距点.
(1)判断:一个内角为120°的菱形是等距四边形.(填“是”或“不是”)
(2)如图2,在5×5的网格图中有A、B两点,请在答题卷给出的两个网格图上各找出C、D两个格点,使得以A、B、C、D为顶点的四边形为互不全等的“等距四边形”,画出相应的“等距四边形”,并写出该等距四边形的端点均为非等距点的对角线长.
端点均为非等距点的对角线长为$\sqrt{10}$ 端点均为非等距点的对角线长为3$\sqrt{2}$
(3)如图1,已知△ABE与△CDE都是等腰直角三角形,∠AEB=∠DEC=90°,连结AD,AC,BC,若四边形ABCD是以A为等距点的等距四边形,求∠BCD的度数.
分析 (1)由菱形的性质和等边三角形的判定与性质即可得出结论;
(2)根据题意画出图形,由勾股定理即可得出答案;
(3)由SAS证明△AEC≌△BED,得出AC=BD,由等距四边形的定义得出AD=AB=AC,证出AD=AB=BD,△ABD是等边三角形,得出∠DAB=60°,由SSS证明△AED≌△AEC,得出∠CAE=∠DAE=15°,求出∠DAC=∠CAE+∠DAE=30°,∠BAC=∠BAE-∠CAE=30°,由等腰三角形的性质和三角形内角和定理求出∠ACB和∠ACD的度数,即可得出答案.
解答 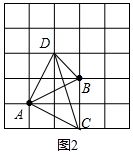 解:(1)一个内角为120°的菱形是等距四边形;
解:(1)一个内角为120°的菱形是等距四边形;
故答案为:是;
(2)如图2,图3所示:
在图2中,由勾股定理得:CD=$\sqrt{{1}^{2}+{3}^{2}}$$\sqrt{10}$;
在图3中,由勾股定理得:CD=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$;
故答案为:$\sqrt{10}$;3$\sqrt{2}$;
(3)解:连接BD.如图1所示:
∵△ABE与△CDE都是等腰直角三角形,
∴DE=EC,AE=EB,
∠DEC+∠BEC=∠AEB+∠BEC,
即∠AEC=∠DEB,
在△AEC和△BED中,$\left\{\begin{array}{l}{DE=CE}&{\;}\\{∠AEC=∠BED}&{\;}\\{AE=BE}&{\;}\end{array}\right.$,
∴△AEC≌△BED(SAS),
∴AC=BD,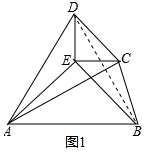
∵四边形ABCD是以A为等距点的等距四边形,
∴AD=AB=AC,
∴AD=AB=BD,
∴△ABD是等边三角形,
∴∠DAB=60°,
∴∠DAE=∠DAB-∠EAB=60°-45°=15°,
在△AED和△AEC中,$\left\{\begin{array}{l}{AD=AC}&{\;}\\{DE=CE}&{\;}\\{AE=AE}&{\;}\end{array}\right.$,
∴△AED≌△AEC(SSS),
∴∠CAE=∠DAE=15°,
∴∠DAC=∠CAE+∠DAE=30°,∠BAC=∠BAE-∠CAE=30°,
∵AB=AC,AC=AD,
∴$∠ACB=\frac{{{{180}°}-{{30}°}}}{2}={75°}$,$∠ACD=\frac{{{{180}°}-{{30}°}}}{2}={75°}$,
∴∠BCD=∠ACB+∠ACD=75°+75°=150°.
点评 本题是四边形综合题目,考查了等距四边形的判定与性质、菱形的性质、等边三角形的判定与性质、勾股定理、全等三角形的判定与性质、等腰三角形的性质、三角形内角和定理等知识;本题综合性强,有一定难度,证明三角形全等是解决问题的关键.


| 序号 | 范围(单位:秒) | 频数 | 频率 |
| 1 | 170<x≤200 | 5 | 0.1 |
| 2 | 200<x≤230 | 13 | a |
| 3 | 230<x≤260 | 15 | 0.3 |
| 4 | 260<x≤290 | c | d |
| 5 | 290<x≤320 | 5 | 0.1 |
| 6 | 320<x≤350 | 2 | 0.04 |
| 7 | 350<x≤380 | 2 | 0.04 |
| 合计 | b | 1.00 |
(2)直接写出a,b,c,d的值.
(3)补全频数直方图.
(4)初中毕业生体能测试项目成绩评定标准是男生1000m不超过4′20″(即260秒)为合格,你能估计出该校初中男生的1000m的合格人数吗?如果能,请求出合格的人数;如果不能,请说明理由.
| 考试成绩/分 | 30 | 29 | 28 | 27 | 26 |
| 学生数/人 | 3 | 15 | 13 | 6 | 3 |
| A. | (-2,3) | B. | (1,-6) | C. | (-3,-2) | D. | (3,3) |
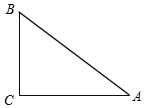 在Rt△ABC中,∠C=90°,AC=4,BC=3,
在Rt△ABC中,∠C=90°,AC=4,BC=3,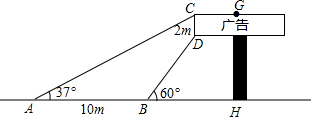 如图,长方形广告牌架在楼房顶部,已知CD=2m,经测量得到∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.(参考数据:tan37°≈0.75,$\sqrt{3}$≈1.732,结果精确到0.1m)
如图,长方形广告牌架在楼房顶部,已知CD=2m,经测量得到∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.(参考数据:tan37°≈0.75,$\sqrt{3}$≈1.732,结果精确到0.1m)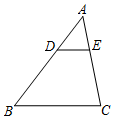 如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E,如果$\frac{AE}{EC}$=$\frac{1}{2}$,DE=7,那么BC的长为21.
如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E,如果$\frac{AE}{EC}$=$\frac{1}{2}$,DE=7,那么BC的长为21.