题目内容
18.解方程:(1)x2-4x+1=0
(2)(x-3)2+4x(x-3)=0.
分析 (1)利用配方法得到(x-2)2=3,然后利用直接开平方法解方程;
(2)利用因式分解法解方程.
解答 解:(1)x2-4x=-1,
x2-4x+4=3,
(x-2)2=3,
x-2=±$\sqrt{3}$,
所以x1=2+$\sqrt{3}$,x2=2-$\sqrt{3}$;
(2)(x-3)(x-3+4x)=0,
x-3=0或x-3+4x=0,
所以x1=3,x2=$\frac{3}{5}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了配方法解一元二次方程.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
10.点(-4,b)与点(a-1,-3)关于x轴对称,则a、b的值分别是( )
| A. | a=-5,b=-3 | B. | a=3,b=3 | C. | a=-3,b=-3 | D. | a=-3,b=3 |
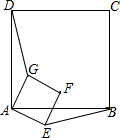 如图,正方形ABCD与正方形AEFG有公共顶点A,当正方形AEFG绕着点A顺时针旋转时,在图中你能否找到一条线段与线段DG相等,并说明理由.
如图,正方形ABCD与正方形AEFG有公共顶点A,当正方形AEFG绕着点A顺时针旋转时,在图中你能否找到一条线段与线段DG相等,并说明理由.