题目内容
19. 如图,AO⊥BO,CO⊥DO,∠AOC=35°,则∠BOD的度数为( )
如图,AO⊥BO,CO⊥DO,∠AOC=35°,则∠BOD的度数为( )| A. | 125° | B. | 135° | C. | 145° | D. | 155° |
分析 由垂线的定义可求得∠AOB=∠COD=90°,然后可求得∠AOD=55°,最后根据∠BOD=∠AOB+∠AOD即可求得答案.
解答 解:∵AO⊥BO,CO⊥DO,
∴∠AOB=∠COD=90°.
∵∠AOC+∠AOD=90°,
∴∠AOD=90°-∠AOC=90°-35°=55°.
∴∠BOD=∠AOB+∠AOD=90°+55°=145°.
故选:C.
点评 本题主要考查的是垂直的定义,掌握图形中角的和差关系是解题的关键.

练习册系列答案
相关题目
10.式子$\frac{1}{x-2}$在实数范围内有意义,则x的取值范围是( )
| A. | x>2 | B. | x≥2 | C. | x≠2 | D. | x≠-2 |
7.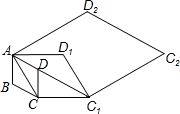 如图,边长为1的菱形ABCD,∠DAB=60°,则菱形ABCD的面积是$\frac{\sqrt{3}}{2}$;连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,则菱形ACC1D1的面积是$\frac{3\sqrt{3}}{2}$;连接对角线AC1,再以AC1为边作第三个菱形AC1C2D,使∠D2AC1=60°,则菱形AC1C2的面积是$\frac{9\sqrt{3}}{2}$;…;按此规律所作的第n个菱形的面积为( )
如图,边长为1的菱形ABCD,∠DAB=60°,则菱形ABCD的面积是$\frac{\sqrt{3}}{2}$;连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,则菱形ACC1D1的面积是$\frac{3\sqrt{3}}{2}$;连接对角线AC1,再以AC1为边作第三个菱形AC1C2D,使∠D2AC1=60°,则菱形AC1C2的面积是$\frac{9\sqrt{3}}{2}$;…;按此规律所作的第n个菱形的面积为( )
 如图,边长为1的菱形ABCD,∠DAB=60°,则菱形ABCD的面积是$\frac{\sqrt{3}}{2}$;连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,则菱形ACC1D1的面积是$\frac{3\sqrt{3}}{2}$;连接对角线AC1,再以AC1为边作第三个菱形AC1C2D,使∠D2AC1=60°,则菱形AC1C2的面积是$\frac{9\sqrt{3}}{2}$;…;按此规律所作的第n个菱形的面积为( )
如图,边长为1的菱形ABCD,∠DAB=60°,则菱形ABCD的面积是$\frac{\sqrt{3}}{2}$;连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,则菱形ACC1D1的面积是$\frac{3\sqrt{3}}{2}$;连接对角线AC1,再以AC1为边作第三个菱形AC1C2D,使∠D2AC1=60°,则菱形AC1C2的面积是$\frac{9\sqrt{3}}{2}$;…;按此规律所作的第n个菱形的面积为( )| A. | $\frac{\sqrt{3}}{2}$×3n | B. | $\frac{\sqrt{3}}{2}$×3n+1 | C. | $\frac{\sqrt{3}}{2}$×3n-1 | D. | $\frac{\sqrt{3}}{2}$×32n-1 |
4.小美将某服饰店的促销活动内容告诉小明后,小明假设某一商品的定价为x元,并列出关系式为0.3(2x-100)<1000,则下列何者可能是小美告诉小明的内容?( )
| A. | 买两件等值的商品可减100元,再打3折,最后不到1000元 | |
| B. | 买两件等值的商品可减100元,再打7折,最后不到1000元 | |
| C. | 买两件等值的商品可打3折,再减100元,最后不到1000元 | |
| D. | 买两件等值的商品可打7折,再减100元,最后不到1000元 |
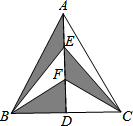 如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的三等分点,若△ABC的面积为12cm2,则图中的阴影面积是6cm2.
如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的三等分点,若△ABC的面积为12cm2,则图中的阴影面积是6cm2.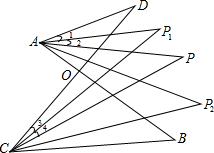 如图中,AP1,AP,AP2是∠DAB的四等分线,CP1,CP,CP2是∠BCD的四等分线,说明∠P与∠P1,P2之间的数量关系.
如图中,AP1,AP,AP2是∠DAB的四等分线,CP1,CP,CP2是∠BCD的四等分线,说明∠P与∠P1,P2之间的数量关系. 如图,在周长为12cm的矩形铁板上剪去一个等边三角形(这个三角形的一边是矩形的宽),则矩形的宽为$\frac{12(4-\sqrt{3})}{13}$cm时,剩下铁板的面积最大.
如图,在周长为12cm的矩形铁板上剪去一个等边三角形(这个三角形的一边是矩形的宽),则矩形的宽为$\frac{12(4-\sqrt{3})}{13}$cm时,剩下铁板的面积最大.