题目内容
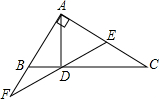
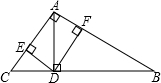 如图,∠BAC=90°,AD⊥BC,DE⊥AC,DF⊥AB,AC=
如图,∠BAC=90°,AD⊥BC,DE⊥AC,DF⊥AB,AC=| 1 |
| 2 |
| 1 |
| 2 |
| A、2对 | B、4对 | C、6对 | D、7对 |
分析:本题根据题意,AC=
BC,则可知∠B=30°,然后根据,∠BAC=90°,AD⊥BC,DE⊥AC,DF⊥AB,进行判断即可.
| 1 |
| 2 |
解答:解:由题意知:∵DE⊥AC,DE⊥AC,∠BAC=90°,∴DE∥AB,DF∥AC.
AC=
BC,则可知∠B=30°,
∵DE∥AB
∴∠CDE=∠B=30°,CE=
CD.
又∵AC=
BC,CE=
CD.
∴AE=
BD.
∵∠B=30°,由题中条件可得:DE⊥AC,AD⊥BC,
∴∠ADF=∠EAD=30°,DE=AF=
AD,DF=
BD,CD=
AC,AD=
AB.
故为六对,
故答案为:C.
AC=
| 1 |
| 2 |
∵DE∥AB
∴∠CDE=∠B=30°,CE=
| 1 |
| 2 |
又∵AC=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=
| 1 |
| 2 |
∵∠B=30°,由题中条件可得:DE⊥AC,AD⊥BC,
∴∠ADF=∠EAD=30°,DE=AF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故为六对,
故答案为:C.
点评:本题考查直角三角形的基本性质,看清图形即可.

练习册系列答案
相关题目
 如图,∠BAC=90°,AD⊥BC,△ABE,△ACF都是等边三角形,则S△ABE:S△ACF等于( )
如图,∠BAC=90°,AD⊥BC,△ABE,△ACF都是等边三角形,则S△ABE:S△ACF等于( )| A、AB:AC | B、AD2:DC2 | C、BD2:DC2 | D、AC2:AB2 |
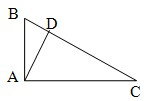 6、如图,∠BAC=90°,AD⊥BC,则图中互余的角有( )
6、如图,∠BAC=90°,AD⊥BC,则图中互余的角有( ) 直线AE与l相交于点D.
直线AE与l相交于点D.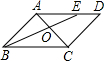
 已知:如图,∠BAC=90°,∠C=30°,AD⊥BC于D,DE⊥AB于E,BE=1,BC=
已知:如图,∠BAC=90°,∠C=30°,AD⊥BC于D,DE⊥AB于E,BE=1,BC=