题目内容
 已知:如图,AB=AC,PB=PC,PD⊥AB,PE⊥AC,垂足分别为D、E.证明:PD=PE.
已知:如图,AB=AC,PB=PC,PD⊥AB,PE⊥AC,垂足分别为D、E.证明:PD=PE.考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:连接AP,利用“SSS”证明△ABP≌△ACP,得出∠PAB=∠PAC,再利用“AAS”定理证明△APD≌△AEP,然后根据全等三角形对应边相等证明即可.
解答:证明:如图:

连接AP,
在△ABP和△ACP中,
∴△ABP≌△ACP,
∴∠PAB=∠PAC,
∵PD⊥AB,PE⊥AC,
∴∠ADP=∠AEP=90°,
在△APD和△AEP中,
∴△APD≌△AEP,
∴PD=PE.

连接AP,
在△ABP和△ACP中,
|
∴△ABP≌△ACP,
∴∠PAB=∠PAC,
∵PD⊥AB,PE⊥AC,
∴∠ADP=∠AEP=90°,
在△APD和△AEP中,
|
∴△APD≌△AEP,
∴PD=PE.
点评:本题考查了全等三角形的判定和性质,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
相关题目
如果分式方程
-
=1有增根,那么增根可能是( )
| 2x |
| x+3 |
| k |
| x2-9 |
| A、-3 | B、3 | C、3或-3 | D、0 |
 如图,C是AB的中点,∠ECA=∠DCB,CD=CE,∠A=40°,求∠B的度数.
如图,C是AB的中点,∠ECA=∠DCB,CD=CE,∠A=40°,求∠B的度数.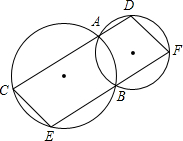 如图,两圆相交于A,B两点,直线CD过点A交两圆于C,D,直线EF交两圆于E,F.探索CE,DF的位置关系.
如图,两圆相交于A,B两点,直线CD过点A交两圆于C,D,直线EF交两圆于E,F.探索CE,DF的位置关系.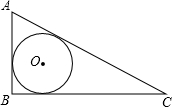 如图,在Rt△ABC中,内切圆⊙O分别与AB、AC、BC相切,且AB=5,AC=13,求内切圆的半径.
如图,在Rt△ABC中,内切圆⊙O分别与AB、AC、BC相切,且AB=5,AC=13,求内切圆的半径. 如图,已知AB=AC,AE=AD,BD=CE,说出∠1=∠2成立的理由.
如图,已知AB=AC,AE=AD,BD=CE,说出∠1=∠2成立的理由.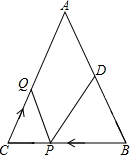 如图,已知△ABC中,∠B=∠C,AB=8厘米,BC=6厘米,点D为AB的中点.如果点P在线段BC上以每秒2厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3).
如图,已知△ABC中,∠B=∠C,AB=8厘米,BC=6厘米,点D为AB的中点.如果点P在线段BC上以每秒2厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3).