��Ŀ����
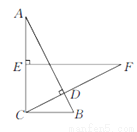
������С��ͬ�ĵ���ֱ�����������ǰ尴ͼ1��ʾ��λ�÷��ã�ͼ2������������ļ���ͼ�Σ�AB=AC��AE=AD����BAC=��EAD=90�㣬B��C��E��ͬһ��ֱ���ϣ�����DC��
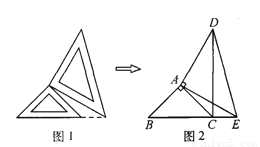
��1�����ҳ�ͼ2�����ABEȫ�ȵ������Σ�������֤����
��2��֤����DC��BE��
��1����ACD�ա�ABE��֤������������2��֤���������� �������� ������������ݵ���ֱ�������ε���������SAS�ж���ABE�ա�ACD����Ϊȫ�������εĶ�Ӧ����ȣ����ԡ�ACD=��ABE=45�㣬��֪��ACB=45�㣬���Կɵõ���BCD=��ACB+��ACD=90�㣬��DC��BE�� �����������1���������� ͼ2�С�ACD�ա�ABE�� ֤�����ߡ�ABC���AED��Ϊ����ֱ��...
��ϰ��ϵ�д�
�����Ŀ


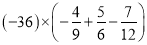 ��
�� 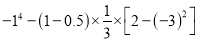 .
.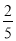 ��xy2��ϵ��Ϊ��
��xy2��ϵ��Ϊ��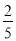 ����1�ǵ���ʽ���۾���ֵ�����������������������ܵ������������������С�1����
����1�ǵ���ʽ���۾���ֵ�����������������������ܵ������������������С�1����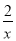 ��5�Ǵ���ʽ������ʽ����2��x2y3�Ĵ���Ϊ7��
��5�Ǵ���ʽ������ʽ����2��x2y3�Ĵ���Ϊ7��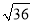 =��6 B. ��
=��6 B. ��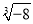 =��2 C.
=��2 C. 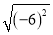 =��6 D.
=��6 D. 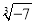 =
=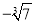
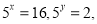 ��
��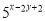 ��ֵ.
��ֵ.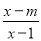 �У���
�У���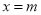 ʱ������˵����ȷ���ǣ� ��
ʱ������˵����ȷ���ǣ� ��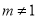 ʱ����ʽ��ֵΪ�� D. ��
ʱ����ʽ��ֵΪ�� D. ��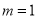 ʱ����ʽ��ֵΪ��
ʱ����ʽ��ֵΪ��