题目内容
13.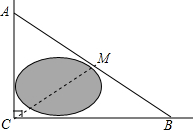 如图,公路AC和BC互相垂直,垂足为点C,公路AB的中点M与点C被湖隔开.已知公路AB=3.2km,则点M,C之间的距离为1.6km.
如图,公路AC和BC互相垂直,垂足为点C,公路AB的中点M与点C被湖隔开.已知公路AB=3.2km,则点M,C之间的距离为1.6km.
分析 根据直角三角形斜边上的中线等于斜边的一半,可得MC=$\frac{1}{2}$AB=1.6km.
解答 解:∵在Rt△ABC中,∠ACB=90°,M为AB的中点,
∴MC=$\frac{1}{2}$AB=1.6km.
故答案为:1.6.
点评 本题考查了直角三角形斜边上的中线的性质:在直角三角形中,斜边上的中线等于斜边的一半.理解题意,将实际问题转化为数学问题是解题的关键.

练习册系列答案
相关题目
3. 如图1,A、B、C三点在正方形网格线的交点处,若将△ACB逆时针旋转得到△AC′B′,则tanB′的值为( )
如图1,A、B、C三点在正方形网格线的交点处,若将△ACB逆时针旋转得到△AC′B′,则tanB′的值为( )
 如图1,A、B、C三点在正方形网格线的交点处,若将△ACB逆时针旋转得到△AC′B′,则tanB′的值为( )
如图1,A、B、C三点在正方形网格线的交点处,若将△ACB逆时针旋转得到△AC′B′,则tanB′的值为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{4}$ |
4.下列四个分式中,是最简分式的是( )
| A. | $\frac{{a}^{2}+{b}^{2}}{a+b}$ | B. | $\frac{{x}^{2}+2x+1}{x+1}$ | C. | $\frac{2ax}{3ay}$ | D. | $\frac{{a}^{2}-{b}^{2}}{a-b}$ |
18.8的立方根是( )
| A. | 2 | B. | ±2 | C. | -2 | D. | 512 |
5.调查显示,截止2015年底某市汽车拥有量为16.9万辆,已知2013年底该市汽车拥有量为10万辆,设2013年底至2015年底该市汽车拥有量的平均增长率为x,根据题意列方程得( )
| A. | 10(1+x)2=16.9 | B. | 10(1+2x)=16.9 | C. | 10(1-x)2=16.9 | D. | 10(1-2x)=16.9 |
2.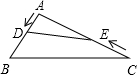 如图,在钝角△ABC中,AB=5cm,AC=10cm,动点D从A点出发到B点止,动点E从C点出发到A点止,点D运动的速度为1cm/秒,点E运动的速度为2cm/秒,如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
如图,在钝角△ABC中,AB=5cm,AC=10cm,动点D从A点出发到B点止,动点E从C点出发到A点止,点D运动的速度为1cm/秒,点E运动的速度为2cm/秒,如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
 如图,在钝角△ABC中,AB=5cm,AC=10cm,动点D从A点出发到B点止,动点E从C点出发到A点止,点D运动的速度为1cm/秒,点E运动的速度为2cm/秒,如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
如图,在钝角△ABC中,AB=5cm,AC=10cm,动点D从A点出发到B点止,动点E从C点出发到A点止,点D运动的速度为1cm/秒,点E运动的速度为2cm/秒,如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )| A. | 2.5秒 | B. | 4.5秒 | C. | 2.5秒或4.5秒 | D. | 2.5秒或4秒 |
3.若关于x的方程(m-2)x2+mx-1=0是一元二次方程,则m的取值范围是( )
| A. | m≠2 | B. | m=2 | C. | m≥2 | D. | m≠0 |
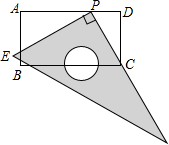 如图,在矩形ABCD中,AB=6,AD=11.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边始终经过点C,另一直角边与AB交于点E.
如图,在矩形ABCD中,AB=6,AD=11.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边始终经过点C,另一直角边与AB交于点E. 如图,某英语单词由四个字母组成,且四个字母都关于直线l对称,则这个英语单词的汉语意思为书.
如图,某英语单词由四个字母组成,且四个字母都关于直线l对称,则这个英语单词的汉语意思为书.