题目内容
5．
如图，在△ABC中，AB=AC，∠A=20°，边AC的垂直平分线交AC于点D，交AB于点E，则∠BCE等于60°．
分析 根据等角对等边可得∠ACB=（180°-20°）÷2=80°，再根据线段垂直平分线的性质可得AE=CE，进而可得∠ACE=∠A=20°，然后可得∠BCE的度数．
解答 解：∵AB=AC，∠A=20°，
∴∠ACB=（180°-20°）÷2=80°，
∵DE是AC的垂直平分线，
∴AE=CE，
∴∠ACE=∠A=20°，
∴∠ECB=80°-20°=60°，
故答案为：60．
点评 此题主要考查了线段垂直平分线的性质，以及等腰三角形的性质，关键是掌握等边对等角．
练习册系列答案
相关题目
解不等式组$\left\{\begin{array}{l}\frac{2x-1}{3}-\frac{5x+1}{2}≤2\\ 5x-1＜3（x+1）\end{array}\right.$并把它的解集在数轴上表示出来．
20．
如图，在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5，过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数y=$\frac{2}{x}$（x≠0）的图象相交于点P1、P2、P3、P4、P5，得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5，并设其面积分别为S1、S2、S3、S4、S5，则S1+S2+S3+S4+S5的值为（ ）
如图，在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5，过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数y=$\frac{2}{x}$（x≠0）的图象相交于点P1、P2、P3、P4、P5，得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5，并设其面积分别为S1、S2、S3、S4、S5，则S1+S2+S3+S4+S5的值为（ ）| A． | 2 | B． | $\frac{137}{60}$ | C． | 3 | D． | $\frac{197}{60}$ |
如图，在平面直角坐标系中，边长不等的正方形依次排列，每个正方形都有一个顶点落在函数y=x的图象上，从左向右第3个正方形中的一个顶点A的坐标为（8，4），阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn，则S10的值为235．
17．计算a2•a5的结果是（ ）
| A． | a10 | B． | a7 | C． | a3 | D． | a8 |
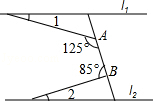如图，直线l1∥l2，∠A=125°，∠B=85°，则∠1+∠2=30°．