Question

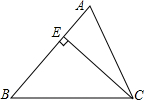如图，△ABC中，CE⊥AB于E，BE=2AE，cosB=

2

3

，BC=3，求tan∠ACE的值．

Answer 1

考点：解直角三角形

专题：

分析：在Rt△BCE中由cosB=

BE

BC

=

2

3

，可设BE=2x，则BC=3x，根据勾股定理求出CE=

5

x；由BE=2AE可得AE=x，在Rt△ACE中利用正切函数的定义即可求出tan∠ACE的值．

解答：解：在Rt△BCE中，∵∠BEC=90°，
∴cosB=

BE

BC

=

2

3

，
∴可设BE=2x，则BC=3x，
根据勾股定理，得CE=

BC2-BE2

=

5

x；
∵BE=2AE=2x，
∴AE=x．
在Rt△ACE中，∵∠AEC=90°，
∴tan∠ACE=

AE

CE

=

x

5 x

=

5

5

．

点评：本题考查了解直角三角形，锐角三角函数的定义，勾股定理，设出适当的未知数，求出CE的值是解题的关键．