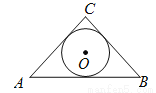
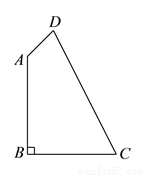
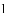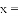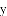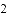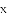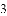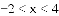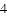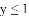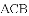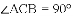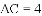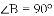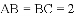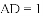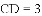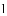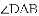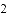题目内容
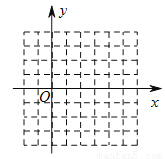
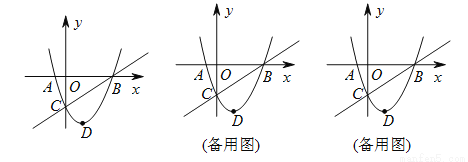
如图,在平面直角坐标系中,二次函数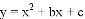 的图像与
的图像与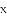
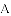
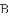
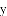
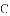
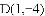
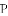
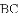
(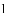
(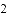
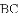
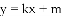
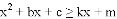 的解集为___________.
的解集为___________.
(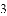
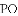
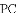
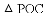
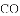
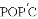 ,那么是否存在点
,那么是否存在点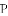
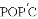 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点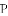
(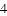
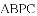
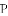
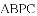
(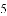
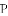
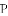
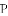
练习册系列答案
相关题目


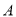 ,
, 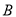 所对应的数是
所对应的数是 ,
, 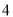 .
.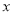 的代数式
的代数式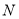 ,我们规定:当有理数
,我们规定:当有理数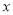 在数轴上所对应的点为
在数轴上所对应的点为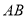 之间(包括点
之间(包括点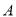 ,
, 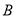 )的任意一点时,代数式
)的任意一点时,代数式 取得所有值的最大值小于等于
取得所有值的最大值小于等于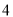 ,最小值大于等于
,最小值大于等于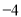 ,则称代数式
,则称代数式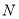 ,是线段
,是线段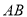 的封闭代数式.
的封闭代数式.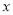 的代数式
的代数式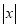 ,当
,当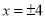 时,代数式
时,代数式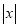 取得最大值是
取得最大值是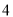 ;当
;当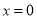 时,代数式
时,代数式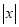 取得最小值是
取得最小值是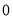 ,所以代数式
,所以代数式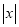 是线段
是线段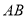 的封闭代数式.
的封闭代数式. )关于
)关于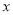 代数式
代数式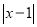 ,当有理数
,当有理数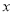 在数轴上所对应的点为
在数轴上所对应的点为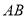 之间(包括点
之间(包括点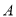 ,
, 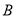 )的任意一点时,取得的最大值和最小值分别是__________.
)的任意一点时,取得的最大值和最小值分别是__________.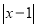 __________(填是或不是)线段
__________(填是或不是)线段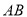 的封闭代数式.
的封闭代数式.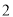 )以下关
)以下关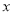 的代数式:
的代数式: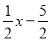 ;②
;②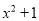 ;③
;③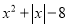 ;④
;④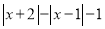 .
.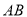 的封闭代数式是__________,并证明(只需要证明是线段
的封闭代数式是__________,并证明(只需要证明是线段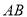 的封闭代数式的式子,不是的不需证明).
的封闭代数式的式子,不是的不需证明).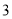 )关于
)关于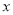 的代数式
的代数式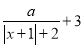 是线段
是线段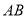 的封闭代数式,则有理数
的封闭代数式,则有理数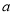 的最大值是__________,最小值是__________.
的最大值是__________,最小值是__________.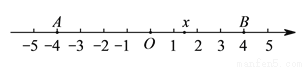
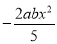 的系数是__________.
的系数是__________.
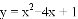 的大致图象(注:图中小正方形网格的边长为
的大致图象(注:图中小正方形网格的边长为