题目内容
【题目】在平面直角坐标系
中，已知点
，
，请确定点C的坐标，使得以A，B，C，O为顶点的四边形是平行四边形，则满足条件的所有点C的坐标是___________．
【答案】(4,0)或(-4,0)或(0,4).
【解析】
需要分类讨论：以AB为该平行四边形的边和对角线两种情况．
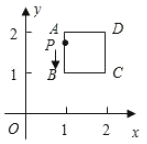
解：如下图所示：
需要对AB分是平行四边形的边长还是对角线两种情况讨论：
情况一：当AB为平行四边形的边时，如上图所示：
根据平行四边形对边相等有AB=OC，
∴C点在x轴上的坐标为：C1(4,0)和C2(-4,0)；
情况二：当AB为平行四边形的对角线时，如上图所示：
此时OC必为平行四边形的另一条对角线，
根据平行四边形对角线互相平分可知，
∴C点在y轴上的坐标为：C3(0,4).
故答案为：(4,0)或(-4,0)或(0,4).
练习册系列答案
相关题目
