Question

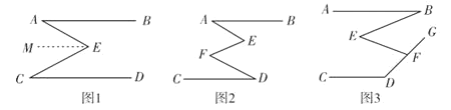
【题目】长江汛期即将来临，为便于夜间查看江水及两岸河堤的情况，防汛指挥部在一危险地带两岸各安置了一探照灯(如图1)，∠BAN=45°.灯A射线自AM顺时针旋转至AN便立即回转，灯B射线自BP顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视.若灯A转动的速度是3度／秒，灯B转动的速度是1度／秒.假定这一带长江两岸河堤是平行的，即PQ∥MN.如图2，两灯同时转动，在灯A射线到达AN之前.若射出的光束交于点C，过C作CD⊥AC交PQ于点D，则在转动过程中，求∠BAC与∠BCD的比值，并说明理由.

Answer 1

【答案】2∠BAC=3∠BCD.

【解析】

设A灯转动时间为t秒，根据A灯的转动速度及邻补角的定义，可用含t的代数式表示出∠CAN，而∠BAN=45°=∠BAC+∠CAN，因此用含t的代数式表示出∠BAC； 再利用平行线的性质，可知∠BCA=∠CBD+∠CAN，用含t的代数式表示出∠BCA，再根据垂直的定义，可证∠BCA+∠BCD=90°，再用含t的代数式表示出∠BCD，然后求出∠BAC与∠BCD的比值，即可得出它们之间的关系.

解：设A灯转动时间为t秒，

∵∠CAN=180°﹣3t，

∴∠BAC=45°﹣（180°﹣3t）=3t﹣135°，

又∵PQ∥MN，

如图，过点C作GH∥PQ∥MN，

则∠HCA=∠CAN,∠BCH=∠CBD,（两直线平行，内错角相等）

∴∠BCA=∠CBD+∠CAN=t+180°﹣3t=180°﹣2t，

而∠ACD=90°，

∴∠BCD=90°﹣∠BCA=90°﹣（180°﹣2t）=2t﹣90°，

即2∠BAC=3∠BCD.