题目内容
若(m+1)x2+2mx﹣1=0是关于x的一元二次方程,则m的值是__________.
是m≠﹣1.
【考点】根的判别式.
【分析】一元二次方程必须满足两个条件:(1)未知数的最高次数是2;(2)二次项系数不为0.由这两个条件得到相应的关系式m+1≠0,再解不等式,进一步结合根的判别式判定即可.
【解答】解:由题意得:m+1≠0,
 解得:m≠﹣1,
解得:m≠﹣1,
且△=b2﹣4ac=4m2+4(m+1)=(2m+1)2+3>0,
方程始终有两个不相等的实数根.
故答案为:m≠﹣1.
【点评】此题主要考查了一元二次方程的概念.只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程,一般形式是ax2+bx+c=0(且a≠0).特别要注意a≠0的条件.以及根的判别式.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 .
.
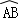 =
=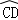 .
.
 B.
B. 且k≠0 C.
且k≠0 C. 且k≠0
且k≠0 ,则a的取值范围是__________.
,则a的取值范围是__________.