题目内容
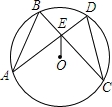
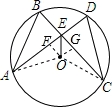
如图,在⊙O中,弦AD、BC相交于点E,连结OE,已知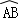 =
=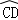 .
.
(1)求证:BE=DE;
(2)如果⊙O的半径为5,AD⊥CB,DE=1,求AE的长.
【考点】圆心角、弧、弦的关系;全等三角形的判定与性质.
【分析】(1)根据圆心角、弧、弦的关系得到AB=CD,推出△ABE≌△CDE,根据全等三角形的性质得到结论;
(2)过O作OF⊥AD与F,OG⊥BC于G,连接OA,OC,根据垂径定理得到AF=FD,BG=OG,由于AD=BC,于是得到AF=CG,推出Rt△AOF≌Rt△OCG,根据全等三角形的性质得到OF=OG,证得四边形OFEG是正方形,于是得到OF=EF,设OF=EF=x,则AF=FD=x+1,根据勾股定理即可得到结论.
【解答】解:(1)∵ =
=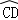 ,
,
∴AB=CD,
在△ABE与△CDE中,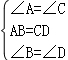 ,
,
∴△ABE≌△CDE,
∴BE=DE;
 (2)过O作OF⊥AD与F,OG⊥BC于G,连接OA,OC,
(2)过O作OF⊥AD与F,OG⊥BC于G,连接OA,OC,
根据垂径定理得:AF=FD,BG=OG,
∵AD=BC,
∴AF=OG,
在Rt△AOF与Rt△OCG中,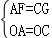 ,
,
∴Rt△AOF≌Rt△OCG,
∴OF=OG,
∵AD⊥CB,
∴四边形OFEG是正方形,
∴OF=EF,
设OF=EF=x,
则AF=FD=x+1,
∴OF2+AF2=OA2,
即:x2+(x+1)2=52,
解得:x=3,x=﹣4(舍去),
∴AF=4,
∴AE=7.
【点评】本题考查了全等三角形的判定和性质,圆心角、弧、弦的关系,勾股定理,熟练则全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
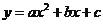 (
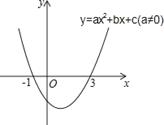
( )的图象如图所示,下列说法:①
)的图象如图所示,下列说法:① ,②当
,②当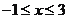 时,
时,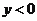 ,③若(
,③若(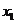 ,
,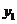 )、(
)、(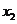 ,
,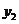 )在函数图象上,当
)在函数图象上,当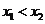 时,
时,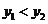 ,④
,④ ,其中正确的是( )
,其中正确的是( )