题目内容
16.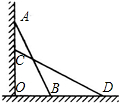 如图,一架云梯AB长25m,斜靠在一竖直的墙AO上,这时梯子底端B离墙的距离BO是7m,如果梯子的顶端A沿墙下滑了4m,那么梯子底部在水平方向也滑动了4m吗?请给以说明.
如图,一架云梯AB长25m,斜靠在一竖直的墙AO上,这时梯子底端B离墙的距离BO是7m,如果梯子的顶端A沿墙下滑了4m,那么梯子底部在水平方向也滑动了4m吗?请给以说明.
分析 首先利用勾股定理在Rt△ABO中计算出AO的长,再在Rt△CDO中利用勾股定理计算出DO的长,进而可得BD的长.
解答 解:梯子底部在水平方向不是滑动了4米,是8米.
在Rt△ABO中,AO=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{2{5}^{2}-{7}^{2}}$=24(米),
∵梯子的顶端A沿墙下滑了4m,
∴AC=4米,
∴CO=20米,
在Rt△CDO中:DO=$\sqrt{C{D}^{2}-C{O}^{2}}$=$\sqrt{625-400}$=15(米),
∴BD=15-7=8(米),
答:梯子底部在水平方向滑动了8米.
点评 此题主要考查了勾股定理的应用,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
7.方程x(x-1)=x的根是( )
| A. | x1=2,x2=0 | B. | x=-2 | C. | x1=-2,x2=0 | D. | x=2 |
4.若x=2是方程ax2-3bx-5=0(a≠0)的根,那么4a-6b的值等于( )
| A. | A4 | B. | 5 | C. | 8 | D. | 10 |
1.下列变形中是因式分解的是( )
| A. | 2x2-1=(2x+1)(2x-1) | B. | x+2y=(x+y)+y | C. | 3x2+6x=3x(x+2) | D. | x2-2x+3=x(x-2)+3 |
 如图,在六边形ABCDEF中,AF∥CD,且∠A=120°,∠B=80°,∠E+∠F=260°,求∠C与∠D的度数.
如图,在六边形ABCDEF中,AF∥CD,且∠A=120°,∠B=80°,∠E+∠F=260°,求∠C与∠D的度数. 如图,在矩形ABCD中,对角线AC与BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE的度数等于75°.
如图,在矩形ABCD中,对角线AC与BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE的度数等于75°.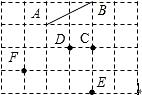 如图,在4×6的正方形网格,点A、B、C、D、E、F都在格点上,连接C、D、E、F中任意两点得到的所有线段中,与线段AB平行的线段是FD,与线段AB垂直的线段是DE.
如图,在4×6的正方形网格,点A、B、C、D、E、F都在格点上,连接C、D、E、F中任意两点得到的所有线段中,与线段AB平行的线段是FD,与线段AB垂直的线段是DE. 如图,直角三角形ABC的斜边AB在数轴上,AC=3,∠ABC=30°.点A对应的数为-2,则点B所对应的数为4.
如图,直角三角形ABC的斜边AB在数轴上,AC=3,∠ABC=30°.点A对应的数为-2,则点B所对应的数为4.