题目内容
6.已知(2x+3)n=1,则x的取值范围是x≠-$\frac{3}{2}$(n=0),x=-1(n是任意整数)或x=-2(n是偶数).分析 首先根据任何非0数的0次幂等于1,可得$\left\{\begin{array}{l}{2x+3≠0}\\{n=0}\end{array}\right.$;然后根据(2x+3)n=1,可得2x+3=1(n是任意整数),或2x+3=-1(n是偶数),据此求出x的取值范围即可.
解答 解:∵(2x+3)n=1,
∴$\left\{\begin{array}{l}{2x+3≠0}\\{n=0}\end{array}\right.$,
∴x≠-$\frac{3}{2}$(n=0);
∵(2x+3)n=1,
∴2x+3=1(n是任意整数),或2x+3=-1(n是偶数),
∴x=-1(n是任意整数),或x=-2(n是偶数),
综上,可得x的取值范围是 x≠-$\frac{3}{2}$(n=0),x=-1(n是任意整数)或x=-2(n是偶数).
故答案为:x≠-$\frac{3}{2}$(n=0),x=-1(n是任意整数)或x=-2(n是偶数).
点评 此题主要考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a0=1(a≠0);②00≠1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.计算${({\sqrt{2}})^2}+1$的结果是( )
| A. | 2 | B. | 3 | C. | $2\sqrt{2}$ | D. | $2\sqrt{2}+1$ |
1.下列计算正确的是( )
| A. | (x2)3=x5 | B. | a+2a=3a2 | C. | (-mn)5÷(-mn)3=m2n2 | D. | a3•a4=a12 |
11.某电视台组织知识竞赛,共设20道选择题,各题分值相同、每题必答,如表记录了五位参赛者的得分情况.
根据表格提供的信息.
(1)每做对一题得5分,每做错一题得-1分;
(2)直接写出m=10,n=64;
(3)参赛者G说他得了80分,你认为可能吗?为什么?
| 参赛者 | A | B | C | D | E |
| 答对题数 | 20 | 19 | 18 | 14 | m |
| 得分 | 100 | 94 | 88 | n | 40 |
(1)每做对一题得5分,每做错一题得-1分;
(2)直接写出m=10,n=64;
(3)参赛者G说他得了80分,你认为可能吗?为什么?
15. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列说法:①abc<0;②2a+b=0;③9a+3b+c>0;④当-1<x<3时,y<0;⑤当x<0时,y随x的增大而减小,其中正确的个数为( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列说法:①abc<0;②2a+b=0;③9a+3b+c>0;④当-1<x<3时,y<0;⑤当x<0时,y随x的增大而减小,其中正确的个数为( )
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列说法:①abc<0;②2a+b=0;③9a+3b+c>0;④当-1<x<3时,y<0;⑤当x<0时,y随x的增大而减小,其中正确的个数为( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列说法:①abc<0;②2a+b=0;③9a+3b+c>0;④当-1<x<3时,y<0;⑤当x<0时,y随x的增大而减小,其中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
16.把2ab2-4ba+2a分解因式的结果是( )
| A. | 2ab(b-2)+2a | B. | 2a(b2-2b) | C. | 2a(b+1)(b-1) | D. | 2a(b-1)2 |
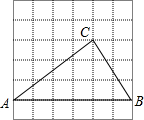 如图,网格中的每个小正方形的边长都是1,△ABC每个顶点都在格点上,则cosA=$\frac{4}{5}$.
如图,网格中的每个小正方形的边长都是1,△ABC每个顶点都在格点上,则cosA=$\frac{4}{5}$.