Question

【题目】如图，从灯塔处观测轮船的位置，测得轮船在灯塔北偏西的方向，轮船在灯塔北偏东的方向，且海里，海里，已知，求、两艘轮船之间的距离.(结果保留根号）

Answer 1

【答案】A、B两艘轮船之间的距离为海里.

【解析】

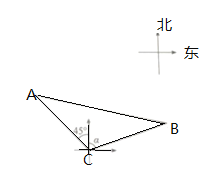
过A点和B点分别作AD⊥MN,BE⊥MN,过B点作BF⊥AD,垂足为D,先求出AD=DC=2，BE=1,CE=3,再求AF,BF的长，由勾股定理即可求出答案.

解：如图，过A点和B点分别作AD⊥MN,BE⊥MN,过B点作BF⊥AD,垂足为D,

∴∠ACD=45°，∠CBE=α,

∵,

∴AD=DC=2,

∵,,设BE=x,则CE=3x,

∴x2+(3x)2=()2,

∴BE=1,CE=3,

∴AF=AD-FD=2,BF=CE+CD=5,

∴AB==,

∴A、B两艘轮船之间的距离为海里.