Question

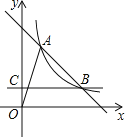
【题目】如图，抛物线y＝ax2＋5ax＋c（a＜0）与x轴负半轴交于A、B两点（点A在点B的左侧），与y轴交于C点，D是抛物线的顶点，过D作DH⊥x轴于点H，延长DH交AC于点E，且S△ABD：S△ACB＝9：16，

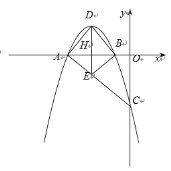
（1）求A、B两点的坐标；

（2）若△DBH与△BEH相似，试求抛物线的解析式．

Answer 1

【答案】(1) ;(2) 见解析.

【解析】

（1） 根据顶点公式求出D坐标(利用a，b，c表示)，得到OC,DH（利用a，b，c表示）值，因为S△ABD：S△ACB＝9：16，所以得到DH:OC=9:16,得到c=4a，利用交点式得出A,B即可.

（2） 由题意可以得到，求出DH,EH(利用a表示),因为 △DBH与△BEH相似，得到，即可求出a（注意舍弃正值），得到解析式.

解：（1） ∴

∵C(0，c) ∴OC=-c，DH= ∵S△ABD：S△ACB＝9∶16

∴ ∴

∴ ∴

（2）① ∵EH∥OC ∴△AEH∽△ACO ∴

∴ ∴

∵ ∵△DBH与△BEH相似

∴∠BDH=∠EBH, 又∵∠BHD=∠BHE=90°∴△DBH∽△BEH

∴ ∴

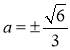∴（舍去正值）

∴