题目内容
已知△ABC是等边三角形,点P是边AC上的一点(点P不与点A,C重合 )PE⊥BC于点E,在CB的延长线上截取BD=PA,连接PD,设PA=nPC.
(1)如图1,若n=1,求EB:BD的值;
(2)如图2,若∠EPD=60°,试求n的值,并求出此时EB:BD的值.
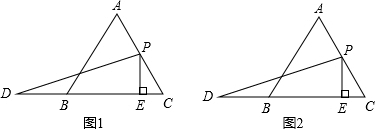
(1)如图1,若n=1,求EB:BD的值;
(2)如图2,若∠EPD=60°,试求n的值,并求出此时EB:BD的值.

考点:相似三角形的判定与性质,等边三角形的性质
专题:
分析:(1)在Rt△PEC中可得到PC和EC的关系,从而可找到AP、BC和EC的关系,则可求得BE:BD的值;
(2)当∠EPD=60°时,可找到AP与EC的关系,可求得n的值,同理用EC表示出BD和BE,可求出比值.
(2)当∠EPD=60°时,可找到AP与EC的关系,可求得n的值,同理用EC表示出BD和BE,可求出比值.
解答:解:(1)当n=1时,即PA=PC,
∵△ABC为等边三角形,
∴∠C=60°,且PE⊥BC,
∴PC=2EC,
∴BD=AP=2EC,BC=AC=2AP=4EC,
∴BE=BC-EC=4EC-EC=3EC,
∴EB:BD=3EC:2EC=3:2;
(2)在Rt△PEC中,∠C=60°,
∴PC=2EC,PE=
EC,
∵∠EPD=60°,
∴在Rt△PED中,DE=
PE=3EC,
∴DC=BC+BD=3EC
∵BD=AP,BC=AC=AP+PC,
∴AP+AP+PC=3EC,
∴2AP=2EC,即AP=EC,
∴AP=
PC,
∴n=
,
此时BD=AP=EC,BE=BC-EC=3EC-EC=2EC,
∴EB:BD=2EC:EC=2:1.
∵△ABC为等边三角形,
∴∠C=60°,且PE⊥BC,
∴PC=2EC,
∴BD=AP=2EC,BC=AC=2AP=4EC,
∴BE=BC-EC=4EC-EC=3EC,
∴EB:BD=3EC:2EC=3:2;
(2)在Rt△PEC中,∠C=60°,
∴PC=2EC,PE=
| 3 |
∵∠EPD=60°,
∴在Rt△PED中,DE=
| 3 |
∴DC=BC+BD=3EC
∵BD=AP,BC=AC=AP+PC,
∴AP+AP+PC=3EC,
∴2AP=2EC,即AP=EC,
∴AP=
| 1 |
| 2 |
∴n=
| 1 |
| 2 |
此时BD=AP=EC,BE=BC-EC=3EC-EC=2EC,
∴EB:BD=2EC:EC=2:1.
点评:本题主要考查等边三角形的性质及含特殊角的直角三角形的性质,利用条件找到AP、PC、BE与EC的关系是解题的关键,注意含30°角的直角三角形的性质的利用.

练习册系列答案
相关题目
下列计算正确的是( )
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
 如图是某学校田径体育场一部分的示意图,跑道的长度是以该跑道的中心线来计算的,如以图中第一道的虚线部分来计算,第一条跑道每圈为400米,跑道分直道和弯道,直道为长相等的平行线段,弯道为同心的半圆型,弯道与直道相连接,已知直道BC的长86.96米,跑道的宽为l米.(π=3.14,结果精确到0.01)
如图是某学校田径体育场一部分的示意图,跑道的长度是以该跑道的中心线来计算的,如以图中第一道的虚线部分来计算,第一条跑道每圈为400米,跑道分直道和弯道,直道为长相等的平行线段,弯道为同心的半圆型,弯道与直道相连接,已知直道BC的长86.96米,跑道的宽为l米.(π=3.14,结果精确到0.01)
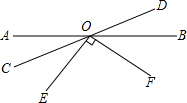 如图,直线AB、CD相交于点O,OC平分∠AOE,OF⊥OE,若∠BOF=n°,求∠DOF的度数.
如图,直线AB、CD相交于点O,OC平分∠AOE,OF⊥OE,若∠BOF=n°,求∠DOF的度数.