题目内容
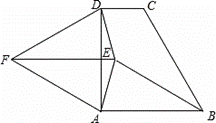
在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,对角线AC与BD相交于
点O,线段OA,OB的中点分别为E,F。 (1)求证:△FOE≌△DOC;
(2)求tan∠BOC的值; (3)设△AGE, △EFO,△BFH的面积分别为S1,S2, S3,
求S1: S2: S3 的值。
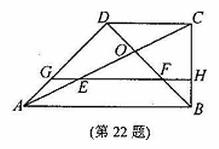
(1)证明:∵EF是△OAB的中位线,
∴EF∥AB,EF=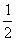 AB,
AB,
 而CD∥AB,CD=
而CD∥AB,CD=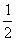 AB,
AB,
∴EF=CD,∠OEF=∠OCD,∠OFE=∠ODC,
∴△FOE≌△DOC;(4分)
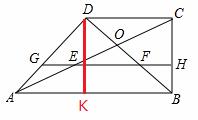
(2) 过点D作DK⊥AB,DK=BC ,BK=DC=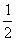 AB=AK,
AB=AK,
∴∠DAB=45°而CD∥AB,∴∠ADC=135°
∵BC=CD, ∠BCD=90°
∴∠DCB=45°
∴∠ADO=90°
∵CD∥AB,∴△DOC∽△BOA
∴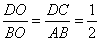 ,设DO=a,则AD=BO=3a
,设DO=a,则AD=BO=3a
∴tan∠BOC=tan∠AOD=3(4分)
(3) ∵ EF∥AB∥CD
∴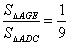 ,
,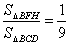 ,而
,而 ∴
∴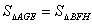
∵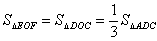 ∴S1: S2: S3= 1:3:1(4分)
∴S1: S2: S3= 1:3:1(4分)

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
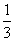 CE时,EP+BP= ;
CE时,EP+BP= ;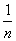 CE时,EP+BP=
CE时,EP+BP= 
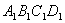 ,
,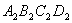 ,
,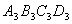 ,…,按如图所示的方式放置.点
,…,按如图所示的方式放置.点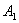 ,
,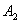 ,
,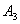 ,…,和点
,…,和点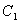 ,
,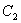 ,
,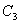 ,…,分别在直线
,…,分别在直线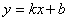 (k>0)和x轴上,已知点
(k>0)和x轴上,已知点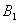 、
、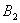 的坐标分别为(1,2),(3,4),则Bn的坐标是( )
的坐标分别为(1,2),(3,4),则Bn的坐标是( )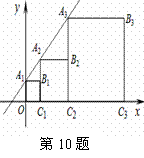
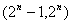 B.
B.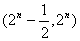 C.
C.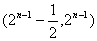 D.
D. 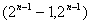
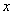 为何值时,代数式
为何值时,代数式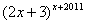 的值为1.
的值为1. =
= 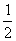 ,则下列正确的是( )
,则下列正确的是( ) B. cosA=
B. cosA=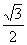 C.tanA=1 D.tanA=
C.tanA=1 D.tanA=
 E,F三点的⊙O的面积为S⊙O,矩形PDEF的面积为S矩形PDEF.
E,F三点的⊙O的面积为S⊙O,矩形PDEF的面积为S矩形PDEF.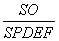 的最小值;
的最小值;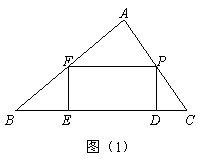
 (3) 当
(3) 当