题目内容
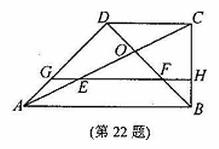
如图,直角梯形ABCD,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边△ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
(1)求证:EB=EF;
(2)四边形ABEF是哪一种特殊四边形?(直接写出特殊四边形名称)
(2)若EF=6,求直角梯形ABCD的面积;
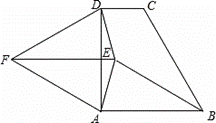
 (1)证明:∵△ADF为等边三角形,
(1)证明:∵△ADF为等边三角形,
∴AF=AD,∠FAD=60°
∵∠DAB=90°,∠EAD=15°,AD=AB
∴∠FAE=∠BAE=75°,AB=AF,
∵AE为公共边
∴△FAE≌△BAE
∴EF=EB
(2)菱形-------3分(写平行四边形2分)
(3)由FA=AB,∠FAE=∠EAB=75°,EA是公共边,
∴△FAE≌△BAE(SAS)
∴BE=EF=6,
又∠AEB=∠AEF=75°,
∴BE=AB=6,
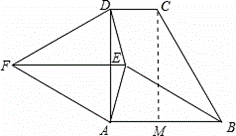
过C作CM⊥AB于M,
CM=AD=6,∠ABC=60°,
∴BM=6/√3=2√3,
∴ CD=6-2√3.
∴梯形ABCD面积=(CD+AB)×AD÷2
=(6-2√3+6)×6÷2
=36-6√3

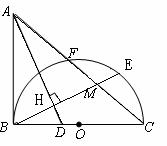
 ,以
,以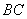 为直径,
为直径,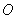 为圆心的半圆交
为圆心的半圆交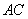 于点
于点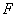 ,点
,点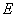 为弧CF的中点,连接
为弧CF的中点,连接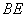 交
交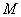 ,
,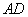 为△ABC的角平分线,且
为△ABC的角平分线,且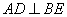 ,垂足为点
,垂足为点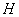 .
. (1)求证:
(1)求证: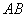 是半圆
是半圆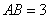 ,
, ,求
,求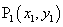 ,
,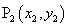 ,……
,……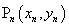 在函数
在函数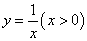 的图像上,
的图像上,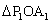 ,
,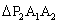 ,
,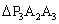 ,……
,……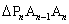 都是等腰直角三角形,斜边
都是等腰直角三角形,斜边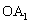 、
、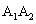 、
、 ,……
,……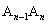 都在
都在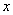 轴上(n是大于或等于2的正整数),则点
轴上(n是大于或等于2的正整数),则点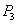 的坐标是 ;点
的坐标是 ;点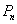 的坐标是 (用含n的式子表示).
的坐标是 (用含n的式子表示).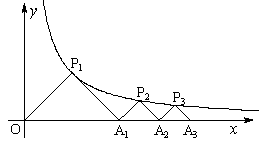
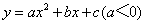 的顶点在线段AB上运动时,形状保持不变,且与x轴交于C,D两点(C在D的左侧),给出下列结论:
的顶点在线段AB上运动时,形状保持不变,且与x轴交于C,D两点(C在D的左侧),给出下列结论: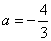 。其中正确的是( )
。其中正确的是( )  且
且 ,则
,则 的取值范围为 ( )
的取值范围为 ( ) B.
B. C.
C. D.
D.
 _________.
_________.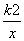 的图像没有公共点,则
的图像没有公共点,则