题目内容
20. 如图,△ABC的边AB与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B,若∠A=30°,求∠C.
如图,△ABC的边AB与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B,若∠A=30°,求∠C.
分析 如图,连接OB,根据切线的性质得∠ABO=90°,则利用互余可得∠AOB=60°,加上∠C=∠OBC,然后利用三角形外角性质可求∠C的度数.
解答 解:如图,连接OB,
∵AB与⊙O相切,
∴OB⊥AB,
∴∠ABO=90°,
∵∠A=30°
∴∠AOB=60°,
∵OB=OC,
∴∠C=∠OBC,
而∠AOB=∠C+∠OBC,
∴∠C=$\frac{1}{2}$∠DOB=30°.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
相关题目
11.下列计算正确的是( )
| A. | x3•x5=x15 | B. | x4÷x=x3 | C. | 3x2•4x2=12x2 | D. | (x5)2=x7 |
5.某外贸企业的职工的工资如下表:
(1)求月工资的平均数;工厂投资者用这个平均数作为代表数,这是为什么?
(2)求月工资的众数;工会主席用众数作为代表数,这是为什么?
(3)求月工资的中位数;税务工作人员用中位数作为代表数,这是为什么?
| 岗位 | 董事长 | 副董事长 | 董事 | 总经理 | 经理 | 部门A | 部门B | 部门C | 部门D | 部门E |
| 人数 | 1 | 1 | 3 | 1 | 4 | 5 | 12 | 20 | 2 | 1 |
| 月工资数(元) | 15000 | 12000 | 10000 | 9000 | 4000 | 2000 | 1800 | 1500 | 800 | 700 |
(2)求月工资的众数;工会主席用众数作为代表数,这是为什么?
(3)求月工资的中位数;税务工作人员用中位数作为代表数,这是为什么?
6.一次函数y=kx+b中的x,y的部分对应值如下表:
根据表中数值分析以下四个结论:
①kb<0;
②y的值随x值的增大而减小;
③方程kx+b=-9的解是x=3;
④当x>-1时,y>7.
其中一定正确的是①②③④.
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | 7 | 3 | -1 | -5 | … |
①kb<0;
②y的值随x值的增大而减小;
③方程kx+b=-9的解是x=3;
④当x>-1时,y>7.
其中一定正确的是①②③④.
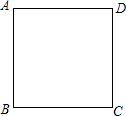 如图,四边形ABCD为正方形.在边AD上取一点E,连接BE,使∠AEB=60°.
如图,四边形ABCD为正方形.在边AD上取一点E,连接BE,使∠AEB=60°. 直线l1∥l2,一块含45°角的直角三角板如图所示放置,∠1=40°,则∠2=85°.
直线l1∥l2,一块含45°角的直角三角板如图所示放置,∠1=40°,则∠2=85°.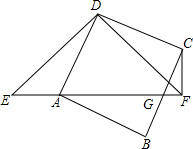 如图,已知在△EDF中,∠EDF=90°,DE=DF,A是EF上的点,以AD为边作正方形ABCD,它的边BC交EF于G点,连接FC.
如图,已知在△EDF中,∠EDF=90°,DE=DF,A是EF上的点,以AD为边作正方形ABCD,它的边BC交EF于G点,连接FC.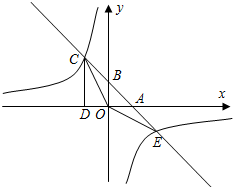 如图,已知一次函数y=k1x+b的图象分别x轴,y轴交于A、B两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OD=1,OE=$\sqrt{10}$,cos∠AOE=$\frac{3\sqrt{10}}{10}$
如图,已知一次函数y=k1x+b的图象分别x轴,y轴交于A、B两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OD=1,OE=$\sqrt{10}$,cos∠AOE=$\frac{3\sqrt{10}}{10}$