题目内容
已知：m、n为两个连续的整数，且m＜
＜n，则m+n= ．
| 29 |
考点：估算无理数的大小
专题：
分析：先估算出
的取值范围，得出m、n的值，进而可得出结论．
| 29 |
解答：解：∵25＜29＜36，
∴5＜
＜6，
∴m=5，n=6，
∴m+n=5+6=11．
故答案为：11．
∴5＜
| 29 |
∴m=5，n=6，
∴m+n=5+6=11．
故答案为：11．
点评：本题考查的是估算无理数的大小，先根据题意算出
的取值范围是解答此题的关键．
| 29 |
练习册系列答案
相关题目
如图，已知⊙O的半径为R．
设a、b、c为实数，x=a2-2b+
，y=b2-2c+
，z=c2-2a+
，则x、y、z中至少有一个值（ ）
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| A、大于0 | B、等于0 |
| C、不大于0 | D、小于0 |
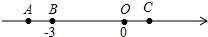如图，数轴上点A、C对应的数分别为a、c，且a、c满足|a+4|+（c-1）2=0．，点B对应的数为-3，