题目内容
建材厂按顾客订货合同生产两种规格的正方形瓷砖,大小两种瓷砖的面积相差319cm2,瓷砖的边长是整数且均不大于50cm,求这两种瓷砖的边长.
考点:因式分解的应用
专题:
分析:设大小两种瓷砖的边长分别为xcm,ycm,则y<x≤50,且x、y都是整数,由题意得x2-y2=319,由319=1×319=11×29,及y<x≤50,得出
,解方程组即可求解.
|
解答:解:设大小两种瓷砖的边长分别为xcm,ycm,则y<x≤50,且x、y都是整数,由题意得
x2-y2=319,
∵319=1×319=11×29,y<x≤50,
∴(x+y)(x-y)=11×29,
∴
,
解得
.
答:大小两种瓷砖的边长分别为25cm,14cm.
x2-y2=319,
∵319=1×319=11×29,y<x≤50,
∴(x+y)(x-y)=11×29,
∴
|
解得
|
答:大小两种瓷砖的边长分别为25cm,14cm.
点评:本题考查了因式分解的应用,平方差公式,根据已知条件得出方程组
是解题的关键.
|

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
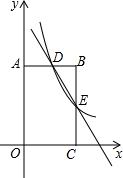 如图,四边形OABC为矩形,以点O为原点建立直角坐标系,点C在x轴的正半轴上,点A在y轴的正半轴上,已知点B为(2,4),反比例函数y=
如图,四边形OABC为矩形,以点O为原点建立直角坐标系,点C在x轴的正半轴上,点A在y轴的正半轴上,已知点B为(2,4),反比例函数y=