题目内容
在△ABC中,∠ABC=30°,AB边长为10,AC边的长度可以在3、5、7、9、11中取值,满足这些条件的互不全等的三角形的个数是( )
| A、3个 | B、4个 | C、5个 | D、6个 |
考点:勾股定理,含30度角的直角三角形
专题:
分析:作出图形,过点A作AD⊥BC于D,根据直角三角形30°角所对的直角边等于斜边的一半可得AD=
AB,然后讨论求解即可.
| 1 |
| 2 |
解答: 解:如图,过点A作AD⊥BC于D,
解:如图,过点A作AD⊥BC于D,
∵∠ABC=30°,AB=10,
∴AD=
AB=5,
当AC=5时,可作1个三角形,
当AC=7时,可作2个三角形,
当AC=9时,可作2个三角形,
当AC=11时,可作1个三角形,
所以,满足条件的互不全等的三角形共有1+2+2+1=6个.
故选D.
 解:如图,过点A作AD⊥BC于D,
解:如图,过点A作AD⊥BC于D,∵∠ABC=30°,AB=10,
∴AD=
| 1 |
| 2 |
当AC=5时,可作1个三角形,
当AC=7时,可作2个三角形,
当AC=9时,可作2个三角形,
当AC=11时,可作1个三角形,
所以,满足条件的互不全等的三角形共有1+2+2+1=6个.
故选D.
点评:本题考查了勾股定理,直角三角形30°角所对的直角边等于斜边的一半,难点在于AC的长度大于AD小于AB时可以作2个三角形.

练习册系列答案
相关题目
 8个一样大小的长方形恰好拼成一个大的长方形(如图1),也可以拼如图2那样的正方形,但这个大正方形中间恰好留下了一个边长为2cm的小正方形.则每一个小长方形的面积为( )
8个一样大小的长方形恰好拼成一个大的长方形(如图1),也可以拼如图2那样的正方形,但这个大正方形中间恰好留下了一个边长为2cm的小正方形.则每一个小长方形的面积为( )| A、32cm2 |
| B、56cm2 |
| C、60cm2 |
| D、64cm2 |
若相距125km的两地在地图上的距离为25cm,则该地图的比例尺为( )
| A、1:500 |
| B、1:50000 |
| C、1:500000 |
| D、1:5000000 |
有下列说法:
①两个无理数的和还是无理数;
②无理数与有理数的和是无理数;
③有理数与有理数的和不可能是无理数.
其中正确的有( )
①两个无理数的和还是无理数;
②无理数与有理数的和是无理数;
③有理数与有理数的和不可能是无理数.
其中正确的有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
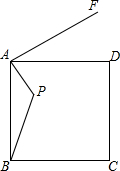 已知点P是边长为5的正方形ABCD内一点,且AP=2,AF⊥AP,垂足是点A,若在射线AF上找一点M,使以点A,M,D为顶点的三角形与△ABP相似,则AM为
已知点P是边长为5的正方形ABCD内一点,且AP=2,AF⊥AP,垂足是点A,若在射线AF上找一点M,使以点A,M,D为顶点的三角形与△ABP相似,则AM为 如图,将正方形纸片的两角分别折叠,使顶点A落在A′处,顶点D落在D,处,BC、BE为折痕,点B、A′、D,在同一条直线上.
如图,将正方形纸片的两角分别折叠,使顶点A落在A′处,顶点D落在D,处,BC、BE为折痕,点B、A′、D,在同一条直线上. 如图,△ABC中,已知,DE∥BC,AE:EC=3:2,求AB:DB,AB:AD的值.
如图,△ABC中,已知,DE∥BC,AE:EC=3:2,求AB:DB,AB:AD的值. 如图,已知
如图,已知