题目内容
16.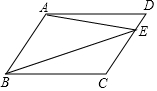 如图,?ABCD的CD边上有一点E,连接AE、BE,∠DAE=12°,∠AEB=33°,则∠EBC的度数是( )
如图,?ABCD的CD边上有一点E,连接AE、BE,∠DAE=12°,∠AEB=33°,则∠EBC的度数是( )| A. | 18° | B. | 21° | C. | 33° | D. | 45° |
分析 由平行四边形的性质得出AD∥EF∥BC,由平行线的性质得出∠AEF=∠DAE=12°,∠BEF=∠EBC,求出∠EBC=∠BEF=21°即可.
解答 解:作EF∥BC交AB于F,如图所示:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵EF∥BC,
∴AD∥EF∥BC,
∴∠AEF=∠DAE=12°,∠BEF=∠EBC,
∵∠AEB=33°,
∴∠EBC=∠BEF=33°-12°=21°;
故选:B.
点评 本题考查了平行四边形的性质、平行线的性质;熟练掌握平行四边形的性质是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11. 如图所示,该几何体的左视图是( )
如图所示,该几何体的左视图是( )
 如图所示,该几何体的左视图是( )
如图所示,该几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
1. 如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )
如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )
 如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )
如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=$\frac{4}{5}\sqrt{5}$;④AF=2$\sqrt{5}$,其中正确结论的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.下列计算正确的是( )
| A. | 2$\sqrt{3}$+3$\sqrt{3}$=5$\sqrt{6}$ | B. | ($\sqrt{2}+1$)(1-$\sqrt{2}$)=1 | C. | (xy)-1($\frac{1}{2}$xy)2=$\frac{1}{4}$xy | D. | -(-a)4÷a2=a2 |
 如图,已知点A、F、C、E在同一直线上,∠1=∠2,AB=DE,请你添加一个条件∠A=∠E(只填一个即可)使△ABC≌△EDF.
如图,已知点A、F、C、E在同一直线上,∠1=∠2,AB=DE,请你添加一个条件∠A=∠E(只填一个即可)使△ABC≌△EDF.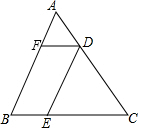 如图,在△ABC中,D、E、F分别是AC、BC、AB上的点,且DE∥AB,DF∥BC,AF:FB=1:4,BC长为20cm,则BE的长为4cm.
如图,在△ABC中,D、E、F分别是AC、BC、AB上的点,且DE∥AB,DF∥BC,AF:FB=1:4,BC长为20cm,则BE的长为4cm.