题目内容
判断对错：关于中心对称的两个图形全等；_____
对
【解析】关于中心对称的两个图形大小形状完全一样.
故答案：对.
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
已知下列命题：
①若a≤0，则|a|=﹣a；
②若ma2＞na2，则m＞n；
③两组对角分别相等的四边形是平行四边形；
④垂直于弦的直径平分弦．
其中原命题与逆命题均为真命题的个数是（ ）
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】①若a≤0，则|a|=﹣a是真命题，逆命题为若|a|=﹣a，则a≤0是真命题，
②若ma2＞na2，则m＞n是真命题，逆命题为若m＞n，则ma2＞na2是假命题，
③两组对角分别相等的四边形是平行四边形是真命题，逆命题为平行四边形的两组对角分别相等是真命题，
④垂直于弦的直径平分弦是真命题，逆命题为平分弦的直径垂直于弦是假命题，
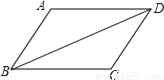
所以原命题与逆命题均为真命... 如图，BD是?ABCD的对角线，过点A作AE⊥BD，垂足为E，过点C作CF⊥BD，垂足为F．
（1）补全图形，并标上相应的字母；
（2）求证：AE=CF．
(1)作图见解析；（2）证明见解析.
【解析】试题分析：（1）根据题意画出图形即可；
（2）由平行四边形的性质得出△ABD的面积=△BCD的面积，得出BD•AE=BD•CF，即可得出结论．
试题解析：（1）如图所示：
（2）∵四边形ABCD是平行四边形，∴△ABD的面积=△BCD的面积，∴BD•AE=BD•CF，∴AE=CF． 如图，有A、B、C三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在( )
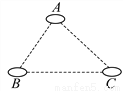
A. 在AC、BC两边高线的交点处 B. 在AC、BC两边中线的交点处
C. 在∠A、∠B两内角平分线的交点处 D. 在AC、BC两边垂直平分线的交点处
D
【解析】根据线段的垂直平分线的性质：线段的垂直平分线上的点到线段的两个端点的距离相等可得：
超市应建在△ABC三条边的垂直平分线的交点处．
故选D． 26个大写英文字母中有多少个是中心对称图形？
7个
【解析】【试题分析】根据中心对称图形的定义可知：把图形度旋转180度，旋转后的图形能喝原来的图形重合进行判断.
【试题解析】分别是H、I、N、O、S、X、Z； 关于中心对称的两个图形对应线段__________________
相等
【解析】关于中心对称的两个图形对应线段长度是相等的.
故答案：相等. 下列说法中正确的是（ ）
A. 能重合的图形一定是成轴对称图形
B. 成中心对称的图形一定是重合的图形
C. 两个成中心对称的图形的对称点连线不一定过对称中心
D. 两个会重合的三角形一定关于某一点成中心对称
B
【解析】试题解析：轴对称图形是沿对称轴折叠重合的图形，而全等的图形即可重合，所以A错误；
中心对称的图形全等即可重合，所以B正确；
成中心对称的图形的对称点连线一定过对称中心，所以C错误；
全等的三角形关于某一点旋转180°后可以重合，才是成中心对称的．所以D错误.
故选B. 分解因式：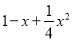 
=____________________.
【解析】1-x+x2=-x+1=( -1)2，
故答案为： . 如图，A，B的坐标为（2，0），（0，1），若将线段AB平移至A1B1，则a+b的值为（ ）
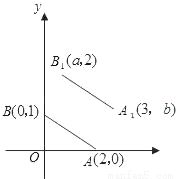
A. 2 B. 3 C. 4 D. 5
A
【解析】由B点平移前后的纵坐标分别为1,2,可得B点向上平移了1个单位,由A点平移前后的横坐标分别是为2,3,可得A点向右平移了1个单位,由此得线段AB的平移的过程是:向上平移1个单位,再向右平移1个单位,所以点A,B均按此规律平移,由此可得a=0+1=1,b=0+1=1,故a+b=2,故选:A.